
 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB.分析 (1)分别以DA,DC,DD1三直线为x,y,z轴,建立空间直角坐标系,求出空间点的坐标,设P(0,1,m),进行数量积的坐标运算求$\overrightarrow{AP}•\overrightarrow{{B}_{1}{D}_{1}}=0$即可;
(2)设平面A1CD的法向量为$\overrightarrow{n}=(x,y,z)$,由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}C}=0}\\{\overrightarrow{n}•\overrightarrow{D{A}_{1}}=0}\end{array}\right.$即可求出法向量$\overrightarrow{n}$,设AD1与平面A1CD所θ,由sinθ=$|cos<\overrightarrow{A{D}_{1}},\overrightarrow{n}>|$即可求得答案.
解答 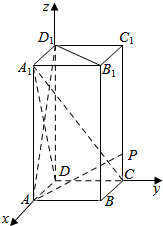 解:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系D-xyz;
解:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系D-xyz;
设AB=1,则:D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,2),A1(1,0,2),B1(1,1,2),C1(0,1,2);
(1)设P(0,1,m),则$\overrightarrow{AP}=(-1,1,m)$,$\overrightarrow{{D_1}{B_1}}=(1,1,0)$;
则$\overrightarrow{AP}•\overrightarrow{{D_1}{B_1}}=0$;
∴AP⊥B1D1;
(2)$\overrightarrow{{A_1}C}=(-1,1,-2),\overrightarrow{D{A_1}}=(1,0,2)$;
设平面A1CD的法向量$\overrightarrow n=(x,y,z)$;
∴$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{{A_1}C}=-x+y-2z=0}\\{\overrightarrow n•\overrightarrow{D{A_1}}=x+2z=0}\end{array}}\right.$;
∴$\left\{\begin{array}{l}{y=0}\\{x=-2z}\end{array}\right.$,令z=1,则$\left\{{\begin{array}{l}{x=-2}\\{y=0}\end{array}}\right.$,∴$\overrightarrow n=(-2,0,1)$,$\overrightarrow{|n}|=\sqrt{5}$;
设AD1与平面A1CD所成的大小为θ,$\overrightarrow{A{D_1}}=(-1,0,2)$,$\overrightarrow{|A{D_1}}|=\sqrt{5}$;
∴$sinθ=|cos<\overrightarrow{A{D_1}},\overrightarrow n>|=\frac{4}{{\sqrt{5}×\sqrt{5}}}=\frac{4}{5}$;
所以AD1与平面A1CD所成角的正弦值为$\frac{4}{5}$.
点评 考查建立空间直角坐标系,利用空间向量证明异面直线垂直及解决线面角问题的方法,能求空间点的坐标,向量垂直的充要条件,以及平面法向量的概念及其求法,线面角的概念,向量夹角余弦的坐标公式.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆、双曲线、圆 | B. | 椭圆、双曲线、抛物线 | ||
| C. | 两条直线、椭圆、圆、双曲线 | D. | 两条直线、椭圆、圆、双曲线、抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 人数xi(人) | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 件数yi(件) | 4 | 7 | 12 | 12 | 20 | 23 | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com