
分析 (1)由已知a1=$\frac{1}{4}$,an+1=$\sqrt{{a}_{n}-{{a}_{n}}^{2}}$,即可得到$0<{a}_{n+1}<\frac{1}{2}$,又0$<{a}_{n}<\frac{1}{2}$,进一步得到${{a}_{n+1}}^{2}-{{a}_{n}}^{2}>0$,则结论an<an+1<$\frac{1}{2}$可证;
(2)首先证当n=2时,$(\frac{{a}_{3}}{{a}_{2}}{)^{2}}^{2}<2$成立,即当n=k时,$(\frac{{a}_{k+1}}{{a}_{k}}{)^{2}}^{k}<2$成立,当n=k+1时,ak+1>ak,则$(\frac{1}{{a}_{k+1}}-1{)^{2}}^{k}<(\frac{1}{{a}_{k}}-1{)^{2}}^{k-1}$=$(\sqrt{\frac{1}{{a}_{k+1}}-1}{)^{2}}^{k}<2$,则结论当n≥2时,($\frac{{a}_{n+1}}{{a}_{n}}$)${\;}^{{2}^{n}}$<2可证.
解答 证明:(1)由${a}_{n}-{{a}_{n}}^{2}≥0$,得${{a}_{n}}^{2}-{a}_{n}≤0$,即0≤an≤1.
∴an+1=$\sqrt{{a}_{n}-{{a}_{n}}^{2}}$=$\sqrt{-({a}_{n}-\frac{1}{2})^{2}+\frac{1}{4}}≤\sqrt{\frac{1}{4}}=\frac{1}{2}$,
又a1=$\frac{1}{4}$≠0,且${a}_{1}≠\frac{1}{2}$,∴0$<{a}_{n}<\frac{1}{2}$.
∴${{a}_{n+1}}^{2}-{{a}_{n}}^{2}={a}_{n}-{{a}_{n}}^{2}-{{a}_{n}}^{2}=-2{{a}_{n}}^{2}+{a}_{n}$>0.
即${a}_{n}<{a}_{n+1}<\frac{1}{2}$;
(2)当n=2时,$(\frac{{a}_{3}}{{a}_{2}}{)^{2}}^{2}=(\frac{\sqrt{{a}_{2}-{{a}_{2}}^{2}}}{{a}_{2}})^{4}=(\frac{1}{{a}_{2}}-1)^{2}$,
又∵${a}_{2}=\sqrt{{a}_{1}-{{a}_{1}}^{2}}=\sqrt{\frac{1}{4}-(\frac{1}{4})^{2}}=\frac{\sqrt{3}}{4}$,
∴$(\frac{1}{{a}_{2}}-1)^{2}=(\frac{4\sqrt{3}-3}{3})^{2}<2$.
即当n=2时,$(\frac{{a}_{3}}{{a}_{2}}{)^{2}}^{2}<2$成立,
当n=k时,$(\frac{{a}_{k+1}}{{a}_{k}}{)^{2}}^{k}<2$成立,即$(\sqrt{\frac{1}{{a}_{k}}-1}{)^{2}}^{k}<2$成立,
当n=k+1时,$(\frac{{a}_{k+2}}{{a}_{k+1}}{)^{2}}^{k+1}=(\sqrt{\frac{1}{{a}_{k+1}}-1}{)^{2}}^{k+1}$=$(\frac{1}{{a}_{k+1}}-1{)^{2}}^{k}$.
∵an+1>an,∴ak+1>ak
∴$\frac{1}{{a}_{k+1}}-1<\frac{1}{{a}_{k}}-1$.
则$(\frac{1}{{a}_{k+1}}-1{)^{2}}^{k}<(\frac{1}{{a}_{k}}-1{)^{2}}^{k-1}$=$(\sqrt{\frac{1}{{a}_{k+1}}-1}{)^{2}}^{k}<2$,
∴当n=k+1时,$(\frac{{a}_{k+2}}{{a}_{k+1}}{)^{2}}^{k+1}<2$也成立,
∴当n≥2时,$(\frac{{a}_{n+1}}{{a}_{n}}{)^{2}}^{n}<2$成立.
点评 本题考查了数列递推式,考查了利用数学归纳法证明结论,本题的计算量大,属于难度较大的题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2tanα | B. | 2tanα | C. | -tanα | D. | tanα |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
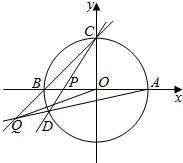 已知直线x+y+1=0被圆O:x2+y2=r2(r>0)所截得的弦长为$\sqrt{2}$.
已知直线x+y+1=0被圆O:x2+y2=r2(r>0)所截得的弦长为$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com