
分析 (Ⅰ)由题意可知$\frac{n}{2}+1=6$,可得n=10,只需令该展开式中x的系数为整数可得;
(Ⅱ)设第Tr+1项的系数最大,可得关于r的不等式组,解不等式组可得r的范围,可得系数最大的项.
解答 解:(Ⅰ)由题意可知$\frac{n}{2}+1=6$,解得n=10,
∴${T_{r+1}}=C_{10}^r{x^{\frac{10-r}{2}}}{2^r}{x^{-2r}}=C_{10}^r{2^r}{x^{\frac{10-5r}{2}}}$,(0≤r≤10,且r∈N),
要求该展开式中的有理项,只需令$\frac{10-5r}{2}∈Z$,
∴r=0,2,4,6,8,10,∴有理项的项数为6项;
(Ⅱ)设第Tr+1项的系数最大,
则$\left\{\begin{array}{l}C_{10}^r{2^r}≥C_{10}^{r-1}{2^{r-1}}\\ C_{10}^r{2^r}≥C_{10}^{r+1}{2^{r+1}}\end{array}\right.$,即$\left\{\begin{array}{l}\frac{2}{r}≥\frac{1}{11-r}\\ \frac{1}{10-r}≥\frac{2}{r+1}\end{array}\right.$,
解不等式可得$\frac{19}{3}≤r≤\frac{22}{3}$,
∵r∈N,∴r=7,
∴展开式中的系数最大的项为${T_8}=C_{10}^7{2^7}{x^{\frac{-25}{2}}}=15360{x^{\frac{-25}{2}}}$
点评 本题考查二项式系数的性质,涉及不等式的解法和组合数公式,属基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 25 | 10 | 35 |
| 女生 | 5 | 10 | 15 |
| 合计 | 30 | 20 | 50 |
| P(Χ2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 97.5% | B. | 99% | C. | 99.5% | D. | 99.9% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{8}{9}$ | C. | $\frac{3}{8}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
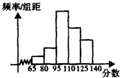 为了解某高三模拟考试学生数学学习情况,从该校参加质检的学生数学成绩中抽取一个样本,并分而5组,绘成如图所示的频率分布直方图,若第二组至第五组数据的频率分别为0.1,0.4,0.3,0.15,第一组数据的频数是2.
为了解某高三模拟考试学生数学学习情况,从该校参加质检的学生数学成绩中抽取一个样本,并分而5组,绘成如图所示的频率分布直方图,若第二组至第五组数据的频率分别为0.1,0.4,0.3,0.15,第一组数据的频数是2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com