
分析 用数学归纳法证明数列问题时分为两个步骤,第一步,先证明当n=1时,结论显然成立,第二步,先假设当n=k+1时,利用此假设证明当n=k+1时,结论也成立即可
解答 解:${S_n}=n{a_1}+\frac{n(n-1)}{2}d,n∈{N^*}$.
下面用数学归纳法证明.1°.n=1时,左边=S1=a1,右边=a1+$\frac{1×0}{2}$d=a1,等式成立.
2°.假设n=k时,等式成立,即Sk=ka1+$\frac{k(k-1)}{2}$d,
当n=k+1时,Sk+1=Sk+ak+1=ka1+$\frac{k(k-1)}{2}$d+a1+kd
=$(k+1){a_1}+\frac{k(k-1)+2k}{2}d$,=$(k+1){a_1}+\frac{(k+1)[(k+1)-1]}{2}d$,
即n=k+1时,等式成立.
综合1°,2°知,对于任意的正整数n,都有Sn=na1+$\frac{n(n-1)}{2}$d成立.
点评 本题主要考查数列递推式、数学归纳法,第(1)问要注意递推公式的灵活运用,第(2)问要注意数学归纳法的证明技巧.数学归纳法的基本形式设P(n)是关于自然数n的命题,若1°P(n0)成立2°假设P(k)成立(k≥n0),可以推出P(k+1)成立,则P(n)对一切大于等于n0的自然数n都成立


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 5 | 4 | 3 | 2 | 4 | 2 |
| A. | 0.70 | B. | 0.60 | C. | 0.45 | D. | 0.35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产的零件中有缺点的零件数随机器运转的速度而变化,如表为抽样数据:
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产的零件中有缺点的零件数随机器运转的速度而变化,如表为抽样数据:| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
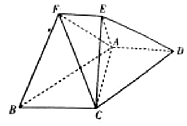 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A12 | B. | A13 | C. | A14 | D. | A15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com