Question

14．一台机器使用的时间较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产的零件中有缺点的零件数随机器运转的速度而变化，如表为抽样数据：

转速x（转/秒）	16	14	12	8
每小时生产有缺点的零件数y（件）	11	9	8	5

（Ⅰ）请画出上表数据的散点图；
（Ⅱ）根据散点图判断，y=ax+b与$y=c\sqrt{x}+d$哪一个适宜作为每小时生产的零件中有缺点的零件数y关于转速x的回归方程类型 （给出判断即可，不必说明理由），根据判断结果及表中数据，建立y关于x的回归方程；
（Ⅲ）若实际生产中，允许每小时生产的零件中有缺点的零件数最多为10个，那么机器的运转速度应控制在什么范围内？
（参考公式：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．）

Answer 1

分析 （Ⅰ）根据所给数据，画出散点图即可；
（Ⅱ）根据散点图求出和规范性方程中的系数，从而求出回归方程即可；
（Ⅲ）解关于x的不等式，求出满足条件的范围即可．

解答 解：（Ⅰ）所作散点图如图：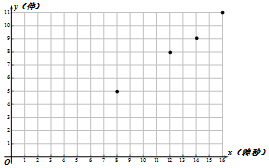

…（2）
（Ⅱ）根据散点图可判断y=ax+b适宜作为每小时生产有缺点的零件数y关于转速x的拟合模型．
…（3分）
相关数据处理如下表：

xi	16	14	12	8	$\overline x=12.5$
yi	11	9	8	5	$\overline y=8.25$
${x_i}^2$	256	196	144	64	$\sum_{i=1}^4{{x_i}^2}=660$
xiyi	176	126	96	40	$\sum_{i=1}^4{{x_i}{y_i}}=438$

…（6分）
所以$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}=\frac{438-4×8.25×12.5}{{660-4×{{12.5}^2}}}$
=0.73．…（8分）
此时，$\hat a=\overline y-b\overline x$=8.25-0.73×12.5=-0.875．…（9分）
于是得到y关于x的回归方程为：$\hat y=0.73x-0.875$．…（10分）
（Ⅲ）由题意可得：$\hat y=0.73x-0.875≤10$，解得x≤14.9，
所以机器的运转速度不能超过14.9转/秒．…（12分）

点评 本小题主要考查散点图、线性与非线回归方程判定、线性回归方程等基础知识，考查运算求解能力、数据处理能力与应用意识，考查化归与转化思想、数形结合思想等．