
| ���ߣ�cm������ | [145��155�� | [155��165�� | [165��175�� | [175��185] |
| ����Ƶ�� | 1 | 5 | 12 | 4 |
| Ů��Ƶ�� | 7 | 15 | 4 | 2 |
���� ������Ƶ�ʷֲ�����������50��ѧ�����ߵ�Ƶ�ʷֲ�ֱ��ͼ��
������Ƶ�ʷֲ�ֱ��ͼ�ܹ�����50��ѧ����ƽ�����ߣ����ܹ�����50��ѧ�����ߵķ��
����������[175��185]��4������Ϊa��b��c��d��2��Ů��ΪA��B�������оٷ����������6��ѧ���������ȡ3��ѧ�������ٳ鵽1��Ů���ĸ��ʣ�
��� �⣺������50��ѧ�����ߵ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��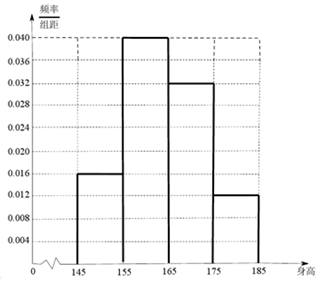
����������ɹ�����50��ѧ����ƽ������Ϊ$\overline x=\frac{150��8+160��20+170��16+180��6}{50}$=164��
���Թ�����50��ѧ�����ߵķ���Ϊs2=$\frac{{8{{��{150-164}��}^2}+20{{��{160-164}��}^2}+16{{��{170-164}��}^2}+6{{��{180-164}��}^2}}}{50}$=80��
���Թ�����50��ѧ�����ߵķ���Ϊ80��
����������[175��185]��4������Ϊa��b��c��d��2��Ů��ΪA��B��
����6��ѧ���������ȡ3��ѧ��������У�
{a��b��c}��{a��b��d}��{a��c��d}��{b��c��d}��{a��b��A}��{a��b��B}��
{a��c��A}��{a��c��B}��{a��d��A}��{a��d��B}��{b��c��A}��{b��c��B}��
{b��d��A}��{b��d��B}��{c��d��A}��{c��d��B}��{a��A��B}��{b��A��B}��
{c��A��B}��{d��A��B}��20�������¼���
�������ٳ鵽1��Ů��������У�
{a��b��A}��{a��b��B}��{a��c��A}��{a��c��B}��{a��d��A}��{a��d��B}��
{b��c��A}��{b��c��B}��{b��d��A}��{b��d��B}��{c��d��A}��{c��d��B}��
{a��A��B}��{b��A��B}��{c��A��B}��{d��A��B}��16�������¼���
�������ٳ鵽1��Ů���ĸ���Ϊ$\frac{16}{20}=\frac{4}{5}$��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã����ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�


 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���� | [10��20�� | [20��30�� | [30��40�� | [40��50�� | [50��60�� | [60��70�� |
| Ƶ�� | 5 | 4 | 3 | 2 | 4 | 2 |
| A�� | 0.70 | B�� | 0.60 | C�� | 0.45 | D�� | 0.35 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 һ̨����ʹ�õ�ʱ��ϳ�����������ʹ�ã�������ͬ��ת������������ij��е�����һЩ����ȱ�㣬ÿСʱ�������������ȱ���������������ת���ٶȶ��仯�����Ϊ�������ݣ�
һ̨����ʹ�õ�ʱ��ϳ�����������ʹ�ã�������ͬ��ת������������ij��е�����һЩ����ȱ�㣬ÿСʱ�������������ȱ���������������ת���ٶȶ��仯�����Ϊ�������ݣ�| ת��x��ת/�룩 | 16 | 14 | 12 | 8 |
| ÿСʱ������ȱ��������y������ | 11 | 9 | 8 | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
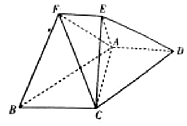 ��֪������ABCDEF�У��ı���ABCDΪƽ���ı��Σ�AD��ƽ��AEC����$AC=\sqrt{2}$��AE=EC=1��AD=2EF��EF��AD��
��֪������ABCDEF�У��ı���ABCDΪƽ���ı��Σ�AD��ƽ��AEC����$AC=\sqrt{2}$��AE=EC=1��AD=2EF��EF��AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\frac{1}{2}$ | C�� | -2 | D�� | $-\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{{\sqrt{3}}}{3}$ | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | $\frac{{\sqrt{2}}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | A12 | B�� | A13 | C�� | A14 | D�� | A15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com