
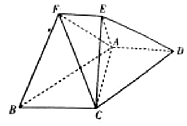
 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.分析 (Ⅰ)证明AD⊥EC.AE⊥EC.推出EC⊥平面ADE,然后证明平面FCE⊥平面ADE.
(Ⅱ)说明AE⊥平面BCEF,通过VABCDEF=VA-BCEF+VD-AEC,转化求解即可.
解答 (Ⅰ)证明:∵AD⊥平面AEC,EC?平面AEC,∴AD⊥EC.
又$AC=\sqrt{2}$,AE=EC=1,∴AC2=AE2+EC2,∴AE⊥EC.
又AE∩AD=A,∴EC⊥平面ADE.∵EC?平面FCE,
∴平面FCE⊥平面ADE.
(Ⅱ)解:易知AE⊥AD,又EF∥AD,∴AE⊥EF,由(Ⅰ)知AE⊥EC,
又EF∩EC=E,∴AE⊥平面BCEF,
又AD=2,∴EF=1.
∴VABCDEF=VA-BCEF+VD-AEC
=$\frac{1}{3}×\frac{1}{2}×({EF+BC})$×EC×EA+$\frac{1}{3}×\frac{1}{2}×AE$×EC×AD
=$\frac{1}{3}×\frac{1}{2}×({1+2})$×$1×1+\frac{1}{3}×\frac{1}{2}$×1×1×2
=$\frac{5}{6}$.
点评 本题考查平面与平面垂直的判定定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$或$\frac{{3\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,3} | B. | {0,3} | C. | {-1,0,3} | D. | {-1,0,3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 身高(cm)分组 | [145,155) | [155,165) | [165,175) | [175,185] |
| 男生频数 | 1 | 5 | 12 | 4 |
| 女生频数 | 7 | 15 | 4 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{8}{9}$ | D. | $\frac{\sqrt{17}}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com