
| 1 |
| 3 |
| a |
| b |
| 4 |
| sin2θ |
| A、1 | B、2 | C、3 | D、4 |
 可先求出曲线与x轴以及x=-1、y轴
可先求出曲线与x轴以及x=-1、y轴| ∫ | 0 -1 |
| 1 |
| 3 |
0 -1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| a |
| b |
| a |
| b |
| 4 |
| sin2θ |
| 4 |
| t |
| 4 |
| t2 |


科目:高中数学 来源: 题型:
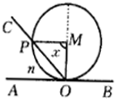 如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )
如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )A、 |
B、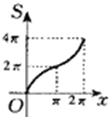 |
C、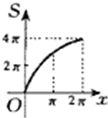 |
D、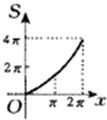 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、“a=3”是“直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直”的充要条件 | ||||||
| B、随机变量ξ~N(0,1),若P(|ξ|≤1.96)=0.950,则P(ξ<-1.96)=0.05 | ||||||
| C、对于命题P:?x∈R使得x2+x+1<0,则¬P:?x∈R均有x2+x+1>0 | ||||||
D、在区间[0,1]上随机取一个数x,则sin
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{x|-1<x<2} |
| B、{x|x>-1} |
| C、{x|-1<x<1} |
| D、{x|1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:
| z1 |
| z2 |
| A、6 | B、-6 | C、-22 | D、22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com