
| A. | x=3,y=10 | B. | x=6,y=10 | C. | x=3,y=15 | D. | x=6,y=15 |
分析 根据平面向量的共线定理,列出方程组,求出x、y的值.
解答 解:∵$\overrightarrow{a}$=(2,x,5),$\overrightarrow{b}$=(4,6,y),且$\overrightarrow{a}$∥$\overrightarrow{b}$,
设$\overrightarrow{a}$=λ$\overrightarrow{b}$,λ∈R,
则$\left\{\begin{array}{l}{2=4λ}\\{x=6λ}\\{5=λy}\end{array}\right.$,
解得$\left\{\begin{array}{l}{λ=\frac{1}{2}}\\{x=3}\\{y=10}\end{array}\right.$,
即x=3,y=10.
故选:A.
点评 本题考查了空间向量的坐标表示与运算问题,也考查了向量共线的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,1) | C. | (1,+∞) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{25}$ | C. | $\frac{1}{15}$ | D. | $\frac{1}{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测的公路北侧一山顶D在西偏北30°的方向上,行驶1200m后到达B处,测得此山顶D在西偏北75°的方向上,仰角为60°,则此山的高度CD=600$\sqrt{6}$m.
如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测的公路北侧一山顶D在西偏北30°的方向上,行驶1200m后到达B处,测得此山顶D在西偏北75°的方向上,仰角为60°,则此山的高度CD=600$\sqrt{6}$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | $[\frac{1}{2},2]$ | C. | $[\frac{1}{2},2016]$ | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
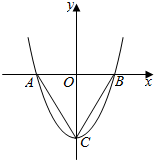 如图.在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A、B,(点A在点B的左侧),与y轴交点C(0,-3).
如图.在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A、B,(点A在点B的左侧),与y轴交点C(0,-3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com