
分析 (I)由2Sn=3an-6n(n∈N*),利用递推关系化为:an+3=3(an-1+3),利用等比数列的通项公式即可得出.
(II)$b{\;}_n=\frac{a_n}{λ^n}$=$\frac{{3}^{n+1}-3}{{λ}^{n}}$,其中常数λ>0,利用数列{bn}为递增数列,可得bn+1>bn,化简即可得出.
解答 解:(I)∵2Sn=3an-6n(n∈N*),∴n=1时,2a1=3a1-6,解得a1=6.
当n≥2时,2an=2(Sn-Sn-1)=3an-6n-[3an-1-6(n-1)],化为:an+3=3(an-1+3).
∴数列{an+3}是等比数列,首项为9,公比为3.
∴an+3=9×3n-1,
∴an=3n+1-3.
(II)$b{\;}_n=\frac{a_n}{λ^n}$=$\frac{{3}^{n+1}-3}{{λ}^{n}}$,其中常数λ>0,
∵数列{bn}为递增数列,
∴bn+1>bn,
∴$\frac{{3}^{n+2}-3}{{λ}^{n+1}}$>$\frac{{3}^{n+1}-3}{{λ}^{n}}$,
化为:λ<$\frac{{3}^{n+1}-1}{{3}^{n}-1}$=3+$\frac{2}{{3}^{n}-1}$.
∵数列$\{\frac{2}{{3}^{n}-1}\}$单调递减,
∴0<λ≤3.
∴λ的取值范围是(0,3].
点评 本题考查了数列的递推关系、等比数列的通项公式、数列的单调性,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
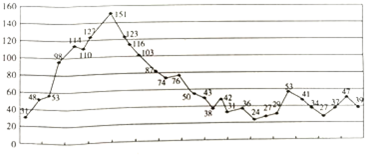
| 空气质量 指数类别 | 优 [0,35] | 良 (35,75] | 轻度污染 (75,115] | 中度污染 (115,150] | 重度污染 (150,250] | 严重污染 (250,500] | 合计 |
| 频数 | 30 | ||||||
| 频率 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
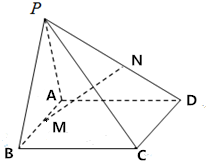 如图,四棱锥P-ABCD中,△ABC与△PAB均为等边三角形,AC=$\sqrt{2}$AD=$\sqrt{2}$CD,PC=$\frac{3}{2}$AB.
如图,四棱锥P-ABCD中,△ABC与△PAB均为等边三角形,AC=$\sqrt{2}$AD=$\sqrt{2}$CD,PC=$\frac{3}{2}$AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com