
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 对选项分别进行判断,即可得出结论.
解答 解:①设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为$\stackrel{∧}{y}$=0.85x-85.71,则若该大学某女生身高增加1cm,则其体重约增加0.85kg,正确;
②命题“?x≥1,x2+3≥4”的否定是“?x≥1,x2+3<4”,不正确;
③相关系数r绝对值越小,表明两个变量相关性越弱,故不正确;
④在一个2×2列联表中,由计算得K2=13.079>10.828,则有99.9%的把握认为这两个变量间有关系,故不正确;
⑤已知随机变量ξ服从正态分布N(2,σ2),P(ξ≤5)=0.79,则P(ξ≤-1)=P(ξ>5)=0.21,正确;
故选:C
点评 本题以命题真假的判断为载体,着重考查了相关系数、命题的否定、正态分布、回归直线方程等知识点,属于中档题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{7}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市教育部门对甲校四年级学生进行体育学科测试,随机抽取15名学生的测试成绩,绘制茎叶图如图:
某市教育部门对甲校四年级学生进行体育学科测试,随机抽取15名学生的测试成绩,绘制茎叶图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
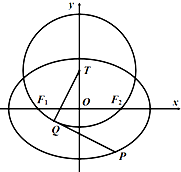 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,若直线3x+4y+5=0上有且仅有一个点M,使得∠F1MF2=90°.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,若直线3x+4y+5=0上有且仅有一个点M,使得∠F1MF2=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com