
分析 (1)设D点坐标为$({\sqrt{2}cosθ,\sqrt{2}sinθ})$,由曲线C在点D处的切线与直线x+y+2=0垂直,求点D的坐标,化为极坐标可得答案;
(2)先求出直线l:y=k(x-2)+2与半圆x2+y2=2(y≥0)相切时k的值,及AB的斜率,进而可得答案.
解答 解:(1)设D点坐标为$({\sqrt{2}cosθ,\sqrt{2}sinθ})$,
由已知得C是以O(0,0)为圆心,$\sqrt{2}$为半径的上半圆,
因为C在点D处的切线与l垂直,
所以直线OD与直线x+y+2=0的斜率相同,即$θ=\frac{3π}{4}$,
故D点的直角坐标为(-1,1),
极坐标为$({\sqrt{2},\frac{3π}{4}})$;
(2)直线l:y=k(x-2)+2与半圆x2+y2=2(y≥0)相切时,$\frac{{|{2k-2}|}}{{\sqrt{1+{k^2}}}}=\sqrt{2}$,
∴k2-4k+1=0,
∴$k=2-\sqrt{3},k=2+\sqrt{3}$(舍去),
设点$B({-\sqrt{2},0})$,则${k_{AB}}=\frac{2-0}{{2+\sqrt{2}}}=2-\sqrt{2}$,
故直线l的斜率的取值范围为$({2-\sqrt{3},2-\sqrt{2}}]$.
点评 本题考查的知识点是参数方程与普通方程的互化,极坐标方程与平面直角坐标方程的互化,直线与圆的位置关系,难度中档.


科目:高中数学 来源: 题型:选择题
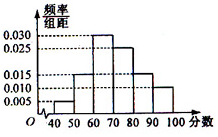 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )| A. | 588 | B. | 480 | C. | 450 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,1] | B. | [0,1] | C. | [$\frac{2}{3}$,+∞) | D. | [1,+∞] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 图象关于点$({-\frac{π}{6},0})$中心对称 | B. | 图象关于$x=-\frac{π}{6}$轴对称 | ||
| C. | 在区间$[{-\frac{5π}{12},-\frac{π}{6}}]$单调递增 | D. | 在$[{-\frac{π}{12},\frac{5π}{12}}]$单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
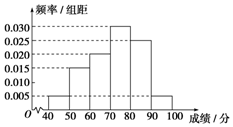 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( )
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( )| A. | 73.3,75,72 | B. | 72,75,73.3 | C. | 75,72,73.3 | D. | 75,73.3,72 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
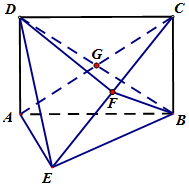 如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点
如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com