
分析 设△ABC,AD是∠A的平分线,AD=2,AB=4,AC=3,根据角平分定理,$\frac{AB}{AC}$=$\frac{BD}{DC}$=$\frac{4}{3}$,设BD=4m,CD=3m,在△ABD和△ADC中,根据余弦定理解得:m2=$\frac{5}{4}$-cos$\frac{A}{2}$,(1),m2=$\frac{13}{9}$-$\frac{4}{3}$cos$\frac{A}{2}$,(2)联立(1)和(2)式,可得:cos$\frac{A}{2}$=$\frac{7}{12}$,从而可求sinA,利用三角形面积公式即可得解.
解答 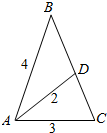 解:设△ABC,AD是∠A的平分线,AD=2,AB=4,AC=3,
解:设△ABC,AD是∠A的平分线,AD=2,AB=4,AC=3,
根据角平分定理,$\frac{AB}{AC}$=$\frac{BD}{DC}$=$\frac{4}{3}$,
设BD=4m,CD=3m,
在△ABD和△ADC中,根据余弦定理,
BD2=AB2+AD2-2×AB×AD×cos$\frac{A}{2}$,可得:16m2=16+4-2×4×2cos$\frac{A}{2}$,解得:m2=$\frac{5}{4}$-cos$\frac{A}{2}$,(1)
CD2=AC2+AD2-2×AC×AD×cos$\frac{A}{2}$,可得:9m2=9+4-2×3×2cos$\frac{A}{2}$,解得:m2=$\frac{13}{9}$-$\frac{4}{3}$cos$\frac{A}{2}$,(2)
比较(1)和(2)式,可得:cos$\frac{A}{2}$=$\frac{7}{12}$,
解得:cosA=2(cos$\frac{A}{2}$)2-1=-$\frac{23}{72}$,sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{7\sqrt{95}}{72}$,
∴S△ABC=$\frac{1}{2}$×AB×AC×sinA=$\frac{1}{2}$×4×3×$\frac{7\sqrt{95}}{72}$=$\frac{7\sqrt{95}}{12}$.
故答案为:$\frac{7\sqrt{95}}{12}$.
点评 本题主要考查了角平分线的性质的应用,考查了余弦定理,三角形面积公式,同角三角函数基本关系式的综合应用,考查了计算能力和转化思想,属于中档题.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:选择题
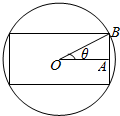 把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )
把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )| A. | y=50cos2θ | B. | y=25sinθ | C. | y=25sin2θ | D. | y=50sin2θ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com