Question

9．已知直三棱柱ABC-A′B′C′中，AB=AC=AA′=2，AB⊥AC，则直三棱柱ABC-A′B′C′的外接球的体积为4$\sqrt{3}$π．

Answer 1

分析 依题意可得△ABC，△A′B′C′的外接圆的圆心O₁，O₂分别是斜边BC，B′C′的中点，
可得直三棱柱ABC-A′B′C′的外接球的球心O为O₁O₂的中点，
球半径R=$\sqrt{O{{O}_{1}}^{2}+{O}_{1}{C}^{2}}$=$\sqrt{{1}^{2}+（\sqrt{2}）^{2}}=\sqrt{3}$，即可求得直三棱柱ABC-A′B′C′的外接球的体积

解答 解：∵AB=AC=2，AB⊥AC，∴△ABC，△A′B′C′的外接圆的圆心O₁，O₂分别是斜边BC，B′C′的中点，
可得直三棱柱ABC-A′B′C′的外接球的球心O为O₁O₂的中点，
球半径R=$\sqrt{O{{O}_{1}}^{2}+{O}_{1}{C}^{2}}$=$\sqrt{{1}^{2}+（\sqrt{2}）^{2}}=\sqrt{3}$．
∴则直三棱柱ABC-A′B′C′的外接球的体积为$\frac{4}{3}π{R}^{3}$=4$\sqrt{3}π$．
故答案为：4$\sqrt{3}$π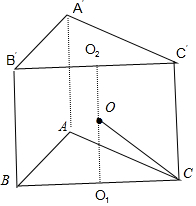

点评 本题给出了直三棱柱，求它的外接球体积，着重考查了直三棱柱的性质、球的体积公式和多面体的外接球等知识，属于基础题．