
| B+C |
| 2 |
| 7 |
| 2 |
| B+C |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,
如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,| AP |
| AB |
| AE |
| A、[-1,1] |
| B、[-1,2] |
| C、[-2,1] |
| D、[0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:
| P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| y1 | y2 | |
| x1 | 15 | 5 |
| x2 | 10 | 15 |
| A、可以在犯错误概率不超过0.025的前提下认为X与Y有关系 |
| B、可以在犯错误概率不超过0.010的前提下认为X与Y有关系 |
| C、可以在犯错误概率不超过0.005的前提下认为X与Y有关系 |
| D、可以在犯错误概率不超过0.001的前提下认为X与Y有关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| 3 |
| b |
| a |
| b |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 室外工作 | 室内工作 | 合计 | |
| 有呼吸系统疾病 | 150 | ||
| 无呼吸系统疾病 | 100 | ||
| 合计 | 200 |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
| P(X2≥k) | 0.050 0.010 |
| k | 3.841 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
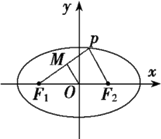 P为椭圆
P为椭圆| x2 |
| 25 |
| y2 |
| 16 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com