
分析 利用正三棱柱的性质找出AD在平面AA1C1C内的射影,进而得到线面角,解直角三角形求出此角的正切值.
解答 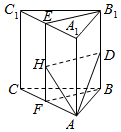 解:如图,取C1A1、CA的中点E、F,
解:如图,取C1A1、CA的中点E、F,
连接B1E与BF,则B1E⊥平面CAA1C1,
过D作DH∥B1E,则DH⊥平面CAA1C1,
连接AH,则∠DAH为AD与平面AA1C1C所成角.
作DE⊥面AA1C1C于E,连接AE,
∵正三棱柱ABC-A1B1C1中已知AB=1,D在棱BB1上,且BD=1,
∴AD=$\sqrt{2}$,DH=B1E=$\frac{\sqrt{3}}{2}$,
∴AH=$\frac{\sqrt{5}}{2}$
∴tan∠DAH=$\frac{DH}{AH}$=$\frac{\sqrt{15}}{5}$
故答案为:$\frac{\sqrt{15}}{5}$.
点评 本题以正三棱柱为载体,考查线面角,关键是找出AD在平面AA1C1C内的射影.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
| A. | 对任意x∈R,都有x 2<ln2 | B. | 不存在x∈R,都有x 2<ln2 | ||
| C. | 存在x∈R,使得x 2≥ln2 | D. | 存在x∈R,使得x 2<ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
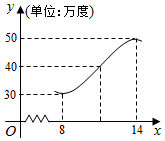 如图,某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b(ω>0,0<φ<π).
如图,某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b(ω>0,0<φ<π).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
| A. | 24 | B. | 35.6 | C. | 40 | D. | 40.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{7}}{7}$或$\frac{5}{7}$ | D. | $\frac{5}{7}$或$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com