解答:
解:(I)f′(x)=3ax
2+2bx+c,由于f(x)在x=1处有极大值2,则
,即
,则c=a+4,b=-2-2a,从而
f′(x)=3ax2+2bx+c=3a(x-1)(x-).
由于f(x)在x=1处有极大值,且a>0,则
>1,即0<a<2.
(1)当
<2,即
<a<2时,x∈(0,1)时,f′(x)>0,∴f(x)在[0,1)上单调递增;
x∈(1,
)时,f′(x)<0,∴f(x)在[1,
)上单调递减;
x∈(
,2)时,f′(x)>0,∴f(x)在[
,2]上单调递增.
(2)当
≥2,即
0<a≤时,x∈(0,1)时,f′(x)>0,∴f(x)在[0,1]上单调递增;
x∈(1,2)时,f′(x)<0,∴f(x)在(1,2]上单调递减.
(II)由于f(x)为[-2,2]上的奇函数,从而b=0,从而f(x)=ax
3+cx,
要使得任意的x∈[-2,2]恒有|f(x)|≤2,则只需任意的x∈[0,2]时|f(x)|≤2恒成立.
显然要使得c取最大值,则c>0.
(1)当a≥0时,则当x∈[0,2]时,f′(x)>0,故f(x)在[0,2]上单调递增.由于任意的x∈[0,2]恒有|f(x)|≤2,则只需f(2)=8a+2c≤2,从而c≤1-4a≤1,即c的最大可能值为1.
(2)当a<0时,则f′(x)=3ax
2+c,令3ax
2+c=0,x=±
.
i)当
≥2时,当x∈[0,2]时,恒有f′(x)≥0,故f(x)在[0,2]上单调递增.要使得任意的x∈[0,2]恒有|f(x)|≤2,则只需f(2)=8a+2c≤2,从而c≤1-4a.
考虑到
≥2,即
-4a≤,从而
c≤1+,故
c≤,即c的最大可能值为
.
ii)当
0<<2时,则当
x∈[0,]时,有f′(x)≥0;当
x∈[,2]时,有f'(x)≤0,从而f(x)在
[0,]上单调递增,在
[,2]上单调递减,故要使得任意的x∈[0,2]恒有|f(x)|≤2,则只需
f()=≤2,且f(2)=8a+2c≥-2
即c
3≤-27a,且
0<-a≤,故
c3≤+,即(c-3)(4c
2+12c+9)=(c-3)(2c+3)
2≤0
故c≤3,即c的最大可能值为3.
由上述可知,c的最大可能值为3.下面我们再证明c=3是可取的,令f(x)=-x
3+3x,x∈[-2,2],则f′(x)=-3x
2+3=-3(x-1)(x+1),则当f′(x)≥0时有-1≤x≤1,故f(x)在[-2,-1]单调递减,在[-1,1]上单调递增,在[1,2]上单调递减,故f
max=max{f(-2),f(1)}=max{2,2}=2,f
min=min{f(-1),f(2)}=min{-2,-2}=-2
从而任意的x∈[-2,2]恒有|f(x)|≤2成立.
综合上述,实数c的最大值为3.



 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案 如图所示,已知四棱锥P-ABCD的底面是菱形,∠DAB=
如图所示,已知四棱锥P-ABCD的底面是菱形,∠DAB=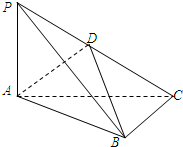 在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=2
在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=2