
分析 由题意,根据三段论的形式“大前提,小前提,结论”直接写出答案即可
解答 解:用三段论的形式写出“因为y=sinx在[0,$\frac{π}{2}$]上是增函数,所以sin$\frac{3π}{7}$>sin$\frac{2π}{5}$”中,”的演绎推理是:
大前提 y=sinx在[0,$\frac{π}{2}$]上是增函数
小前提 $\frac{3π}{7}$>$\frac{2π}{5}$ 且 $\frac{3π}{7}$,$\frac{2π}{5}$∈[0,$\frac{π}{2}$]
结论 sin$\frac{3π}{7}$>sin$\frac{2π}{5}$
故答案为:y=sinx在[0,$\frac{π}{2}$]上是增函数,$\frac{3π}{7}$>$\frac{2π}{5}$ 且 $\frac{3π}{7}$,$\frac{2π}{5}$∈[0,$\frac{π}{2}$],sin$\frac{3π}{7}$>sin$\frac{2π}{5}$
点评 本题考查演绎推理--三段论,解题的关键是理解三段论的形式,本题是基础概念考查题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
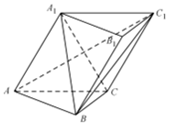 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{3}$ | B. | -$\frac{7}{6}$ | C. | -$\frac{7}{3}$ | D. | -$\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com