
分析 (Ⅰ)由已知和余弦定理可得cosA=$\frac{1}{2}$,可得$A=\frac{π}{3}$;
(Ⅱ)由题意和三角函数公式可得$f(B)=sin(B+\frac{π}{3})+\frac{{\sqrt{3}}}{2}$,由三角函数的最值可得$B=\frac{π}{6}$,可判△ABC是直角三角形.
解答 解:(Ⅰ)∵在△ABC中,b2+c2-a2=bc,
∴由余弦定理可得$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{1}{2}$,
∵A∈(0,π),∴$A=\frac{π}{3}$;
(Ⅱ)∵$f(x)=sin\frac{x}{2}cos\frac{x}{2}+\sqrt{3}{cos^2}\frac{x}{2}$,
∴$f(x)=\frac{1}{2}sinx+\frac{{\sqrt{3}}}{2}cos+\frac{{\sqrt{3}}}{2}$,
∴$f(x)=sin(x+\frac{π}{3})+\frac{{\sqrt{3}}}{2}$,
∴$f(B)=sin(B+\frac{π}{3})+\frac{{\sqrt{3}}}{2}$,
∵B∈(0,π),∴当$B+\frac{π}{3}=\frac{π}{2}$,
即$B=\frac{π}{6}$时,f(B)取最大值,
∴此时易知道△ABC是直角三角形.
点评 本题考查正余弦定理解三角形,涉及三角形形状的判断,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 31 | C. | 63 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
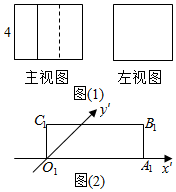 某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形O1A1B1C1如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )
某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形O1A1B1C1如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )| A. | 48 | B. | 64 | C. | 96 | D. | 128 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com