
分析 (I)令f(x)=0解出;
(II)根据f(x)的函数类型和图象开口讨论,只需fmin(x)<0即可;
(III)对函数类型,开口方向,单调性进行讨论,令fmin(x)≥0列出不等式,根据不等式的性质得出a+b的范围.
解答 解:(I)a=b=1时,f(x)=2x2+x,令f(x)=0,解得x=0或x=-$\frac{1}{2}$.∴f(x)的零点为0,-$\frac{1}{2}$.
(II)当b=$\frac{4}{3}$时,f(x)=2ax2+$\frac{4}{3}$x-a+1,
①当a=0时,f(x)=$\frac{4}{3}x$+1,f(x)为R上的增函数,f(-$\frac{3}{4}$)=0,∴当x0<-$\frac{3}{4}$时,f(x0)<0,符合题意;
②当a<0时,f(x)的图象开口向下,显然存在x0∈R,使得f(x0)<0,符合题意;
③当a>0时,f(x)的图象开口向上,对称轴为x=-$\frac{1}{3a}$,fmin(x)=f(-$\frac{1}{3a}$)=1-a-$\frac{2}{9a}$,
令1-a-$\frac{2}{9a}$<0,解得a$>\frac{2}{3}$或0<a<$\frac{1}{3}$.
综上,a的取值范围是(-∞,$\frac{1}{3}$)∪($\frac{2}{3}$,+∞).
(III)①若a=0,f(x)=bx+1,
当b=0时,f(x)=1,符合题意,此时,a+b=0,
当b>0时,f(x)在[-1,1]上是增函数,∴fmin(x)=f(-1)=-b+1≥0,∴b≤1,此时,a+b=b≤1.
当b<0时,f(x)在[-1,1]上是减函数,∴fmin(x)=f(1)=b+1≥0,∴-1≤b<0,此时a+b=b<0.
②若a>0,f(x)图象开口向上,对称轴为x=-$\frac{b}{4a}$,
当-$\frac{b}{4a}$≤-1即4a-b≤0时,f(x)在[-1,1]上是增函数,fmin(x)=f(-1)=a-b+1≥0,∴b-a≤1.
由$\left\{\begin{array}{l}{4a-b≤0}\\{b-a≤1}\\{a>0}\end{array}\right.$得$\left\{\begin{array}{l}{0<a≤\frac{1}{3}}\\{b≤\frac{4}{3}}\end{array}\right.$,∴a+b≤$\frac{5}{3}$.
当-$\frac{b}{4a}$≥1即4a+b≤0时,f(x)在[-1,1]上是减函数,fmin(x)=f(1)=a+b+1≥0,∴-a-b≤1.
由$\left\{\begin{array}{l}{4a+b≤0}\\{-a-b≤1}\\{a>0}\end{array}\right.$得$\left\{\begin{array}{l}{0<a≤\frac{1}{3}}\\{-\frac{4}{3}≤b<0}\end{array}\right.$,∴a+b<$\frac{1}{3}$.
当-1<-$\frac{b}{4a}$<1即-4a<b<4a时,f(x)在[-1,1]上先减后增,fmin(x)=f(-$\frac{b}{4a}$)=-$\frac{{b}^{2}}{8a}$-a+1≥0,∴$\frac{{b}^{2}}{8a}$+a≤1,
由-4a<b<4a得b2<16a2,∴3a≤1,∴0$<a≤\frac{1}{3}$.∴a+b<5a≤$\frac{5}{3}$.
③若a<0,f(x)图象开口向下,对称轴为x=-$\frac{b}{4a}$,
当-$\frac{b}{4a}$≤-1即4a-b≥0时,f(x)在[-1,1]上是减函数,fmin(x)=f(1)=a+b+1≥0,∴a+b≥-1.
由$\left\{\begin{array}{l}{4a-b≥0}\\{a+b≥-1}\\{a<0}\end{array}\right.$得-$\frac{1}{5}$≤a<0,又∵b≤4a,∴a+b≤5a<0.
当-$\frac{b}{4a}$≥1即4a+b≥0时,f(x)在[-1,1]上是增函数,fmin(x)=f(-1)=a-b+1≥0,∴a-b≥-1,
由$\left\{\begin{array}{l}{4a+b≥0}\\{a-b≥-1}\\{a<0}\end{array}\right.$得-$\frac{1}{5}$≤a<0,又∵b≤a+1,∴a+b≤2a+1<1.
当-1<-$\frac{b}{4a}$<1即4a<b<-4a时,f(x)在[-1,1]上先增后减,
f(1)=a+b+1≥0.f(-1)=a-b+1≥0,两式相加得-1≤a<0,.∴b≤a+1,∴a+b≤2a+1<1.
综上,a+b的最大值为$\frac{5}{3}$.
点评 本题考查了函数的零点,一元二次函数的单调性,函数恒成立的条件,分类讨论思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
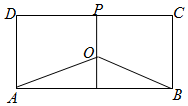 节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.
节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c至少与a、b中的一条相交 | B. | c至多与a、b中的一条相交 | ||
| C. | c与a、b都相交 | D. | c与a、b都不相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{6}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com