Question

15．小明每天早上在6：30～7：30之间离开家去上学，小强每天早上6：00～7：00之间到达小明家，约小明一同前往学校，则小强能见到小明的概率是（　　）

• A． 1
• B． $\frac{3}{8}$
• C． $\frac{7}{8}$
• D． $\frac{1}{8}$

Answer 1

分析 设小明离开家去上学的时间为x，小强到达小明家的时间为y，建立平面直角坐标系，则（x，y）可以看成平面中的点，分析可得由试验的全部结果所构成的区域并求出其面积，同理可得小强能见到小明（事件A）事件所构成的区域及其面积，由几何概型公式，计算可得答案．

解答 解：设小明离开家去上学的时间为x，小强到达小明家的时间为y，
可得由试验的全部结果满足条件为$\left\{\begin{array}{l}{6.5≤x≤7.5}\\{6≤y≤7}\end{array}\right.$，所构成的区域的面积为s=1×1=1．
可得小强能见到小明（事件A）事件满足条件$\left\{\begin{array}{l}{6.5≤x≤7.5}\\{6≤y≤7}\\{x≤y}\end{array}\right.$，所构成的区域的面积为s′=1-$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}=\frac{7}{8}$．
故选：C．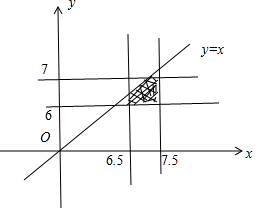

点评 本题考查几何概型的会面问题，准确作图利用面积作为几何测度是解决问题的关键，属中档题．