Question

3．如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，△PAB为等边三角形，O为AB的中点，PO丄AC．
（1）求证：平面PAB丄平面ABCD；
（2）求PC与平面ABCD所成角的余弦值．

Answer 1

分析 （1）要证明平面PAB⊥平面ABCD，根据面面垂直的判定定理，关键是要在一个平面里找到一条直线与另外一个平面垂直，观察发现△PAB底边AB上的中线满足要求，添加辅助线后，证明线面垂直即可得到结论．
（2）由（1）的结论，我们易得∠PCO即为所求，构造三角形，解三角形即可得到答案．

解答 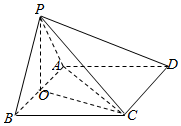解：（1）证明：∵△PAB为等边三角形，O为AB中点，
∴PO⊥AB．
又PO⊥AC，∴PO⊥平面ABCD．
又PO?平面PAB，
∴平面PAB⊥平面ABCD．
（2）解：∵PO⊥平面ABCD．
∴∠PCO为直线PC与平面ABCD所成的角．
设底面正方形边长为2，
则PO=$\sqrt{3}$，CO=$\sqrt{5}$∴PC=$\sqrt{P{O}^{2}+C{O}^{2}}=2\sqrt{2}$，cos∠PCO=$\frac{CO}{PC}=\frac{\sqrt{5}}{2\sqrt{2}}=\frac{\sqrt{10}}{4}$
∴PC与平面ABCD所成角的余弦值为$\frac{\sqrt{10}}{4}$．

点评 本小题主要考查空间面面关系的垂直关系的判断、线面角的求解，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、属于中档题．