Question

13．在△ABC中，内角A，B，C的对边分别为a，b，c，且b=1，c=2，∠C=60°，若D是边BC上一点且∠B=∠DAC，则AD=$\frac{\sqrt{13}-1}{3}$．

Answer 1

分析 在△ABC中使用正弦定理解出B，得出sin∠ADC，在△ACD中使用正弦定理解出AD．

解答 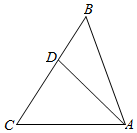解在△ABC中，由正弦定理得$\frac{b}{sinB}=\frac{c}{sinC}$，即$\frac{1}{sinB}=\frac{2}{\frac{\sqrt{3}}{2}}$，
解得sinB=$\frac{\sqrt{3}}{4}$．∴cosB=$\frac{\sqrt{13}}{4}$．
∴sin∠BAC=sin（B+C）=sinBcosC+cosBsinC=$\frac{\sqrt{39}+\sqrt{3}}{8}$．
∵∠B=∠DAC，∴∠ADC=∠B+∠BAD=∠DAC+∠BAD=∠BAC．
∴sin∠ADC=sin∠BAC=$\frac{\sqrt{39}+\sqrt{3}}{8}$．
在△ACD中，由正弦定理得$\frac{AC}{sin∠ADC}=\frac{AD}{sinC}$，即$\frac{1}{\frac{\sqrt{39}+\sqrt{3}}{8}}=\frac{AD}{\frac{\sqrt{3}}{2}}$，
解得AD=$\frac{\sqrt{13}-1}{3}$．
故答案为$\frac{\sqrt{13}-1}{3}$．

点评 本题考查了正弦定理在解三角形中的应用，属于中档题．