
分析 (1)由题意可得即 g(x)<-a恒成立,作出函数g(x)的图象,求得函数g(x)的最大值为g(x)max=1,可得-a>1,∴从而求得a的范围.
(2)在同一坐标系内作出函数g(x)=|x+1|-|x|图象和y=x的图象,由题意可知,把函数y=g(x)的图象向下平移1个单位以内(不包括1个单位),则它与y=x的图象始终有3个交点,从而得到a的范围.
解答 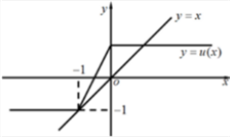 解:(1)令g(x)=|x+1|-|x|,则由题意可得f(x)≥0的解集为∅,即g(x)≥-a的解集为∅,
解:(1)令g(x)=|x+1|-|x|,则由题意可得f(x)≥0的解集为∅,即g(x)≥-a的解集为∅,
即 g(x)<-a恒成立.
∵$g(x)=|x+1|-|x|=\left\{\begin{array}{l}-1,x<-1\\ 2x+1,-1≤x<0\\ 1,x≥0\end{array}\right.$,作出函数g(x)的图象,
由图可知,函数g(x)的最小值为g(x)min=-1;函数g(x)的最大值为g(x)max=1.
∴-a>1,∴a<-1,
综上,实数a的取值范围为(-∞,-1).
(2)在同一坐标系内作出函数g(x)=|x+1|-|x|图象和y=x的图象如下图所示,由题意可知,
把函数y=g(x)的图象向下平移1个单位以内(不包括1个单位)与y=x的图象始终有3个交点,
从而-1<a<0.
点评 本题主要考查分段函数的应用,函数的恒成立问题,方程根的存在性以及个数判断,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
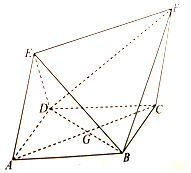 如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.
如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
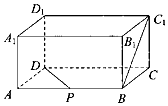 如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成角等于( )
如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{\sqrt{2e}}{e}$+2) | B. | (1,$\frac{\sqrt{2e}}{e}$+1) | C. | (1,$\frac{\sqrt{2e}}{2e}$+1) | D. | (2,$\frac{\sqrt{2e}}{2e}$+2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 12 | C. | 21 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8};\frac{π}{4}$ | B. | $\frac{1}{4};\frac{π}{2}$ | C. | $\frac{1}{2};π$ | D. | 1;2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com