
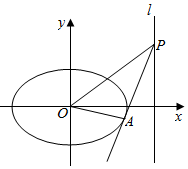
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1),过直线l:x=2上一点P作椭圆的切线,切点为A,当P点在x轴上时,切线PA的斜率为±$\frac{{\sqrt{2}}}{2}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1),过直线l:x=2上一点P作椭圆的切线,切点为A,当P点在x轴上时,切线PA的斜率为±$\frac{{\sqrt{2}}}{2}$.分析 (Ⅰ)由P在x轴设出P点坐标及直线PA方程,将PA方程与椭圆方程联立,整理关于x的一元二次方程,△=0求得a2,即可求得椭圆方程;
(Ⅱ)设出切线方程和点P及点A的坐标,将切线方程代入椭圆方程,求得关于x的一元二次方程,△=0,求得A和P点的坐标,求得丨PO丨及A到直线OP的距离,根据三角形的面积公式求得S=丨k+$\sqrt{1+2{k}^{2}}$丨,平方整理关于k的一元二次方程,△≥0,即可求得S的最小值.
解答  解:(1)当P点在x轴上时,P(2,0),PA:$y=±\frac{{\sqrt{2}}}{2}(x-2)$,
解:(1)当P点在x轴上时,P(2,0),PA:$y=±\frac{{\sqrt{2}}}{2}(x-2)$,
$\left\{\begin{array}{l}y=±\frac{{\sqrt{2}}}{2}(x-2)\\ \frac{x^2}{a^2}+{y^2}=1\end{array}\right.⇒(\frac{1}{a^2}+\frac{1}{2}){x^2}-2x+1=0$,
△=0⇒a2=2,椭圆方程为$\frac{x^2}{2}+{y^2}=1$;…-5
(2)设切线为y=kx+m,设P(2,y0),A(x1,y1),
则$\left\{\begin{array}{l}y=kx+m\\{x^2}+2{y^2}-2=0\end{array}\right.$⇒(1+2k2)x2+4kmx+2m2-2=0⇒△=0⇒m2=2k2+1,…7
且${x_1}=\frac{-2km}{{1+2{k^2}}},{y_1}=\frac{m}{{1+2{k^2}}}$,y0=2k+m
则$|PO|=\sqrt{{y_0}^2+4}$,
PO直线为$y=\frac{y_0}{2}x⇒$,A到直线PO距离$d=\frac{{|{y_0}{x_1}-2{y_1}|}}{{\sqrt{{y_0}^2+4}}}$,…-10
则${S_{△POA}}=\frac{1}{2}|PA|•d=\frac{1}{2}|{y_0}{x_1}-2{y_1}|=\frac{1}{2}|(2k+m)\frac{-2km}{{1+2{k^2}}}-\frac{2m}{{1+2{k^2}}}|$
=$|\frac{{1+2{k^2}+km}}{{1+2{k^2}}}m|=|k+m|=|k+\sqrt{1+2{k^2}}|$,…13
∴(S-k)2=1+2k2⇒k2+2Sk-S2+1=0,
$△=8{S^2}-4≥0⇒S≥\frac{{\sqrt{2}}}{2}$,此时$k=±\frac{{\sqrt{2}}}{2}$.…-15
点评 本题考查曲线方程的求法,考查三角形面积的最小值的求法,综合性强,难度大,解题时要注意推理论证能力的培养,属于中档题.


 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:解答题
 如图,矩形OABC内的阴影部分由直线f(x)=sinx及直线x=a(a∈(0,2π))与x轴围成.向矩形OABC内随机掷一点,该点落在阴影部分的概率为$\frac{1}{2}$,求函数h(x)=x-f(x)在[0,a]上的值域.
如图,矩形OABC内的阴影部分由直线f(x)=sinx及直线x=a(a∈(0,2π))与x轴围成.向矩形OABC内随机掷一点,该点落在阴影部分的概率为$\frac{1}{2}$,求函数h(x)=x-f(x)在[0,a]上的值域.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ξ | B. | ξ-μ | C. | $\frac{ξ+μ}{σ}$ | D. | $\frac{ξ-μ}{σ}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com