
 如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.分析 (Ⅰ)由AB是直径,可得BC⊥AC,再由CD⊥平面ABC,得CD⊥BC,由线面垂直的判定可得BC⊥平面ACD,结合面面垂直的判定得平面ADE⊥平面ACD;
(Ⅱ)建立如图所示空间直角坐标系,求出D,E,A的坐标,进一步求得面DAE的法向量$\overrightarrow{{n}_{1}}=(1,0,2\sqrt{2})$,由题意可知平面ABE的法向量为$\overrightarrow{{n}_{2}}=\overrightarrow{CO}=(\sqrt{2},\sqrt{2},0)$,求出两法向量所成角的余弦值,得到二面角D-AE-B的余弦值.
解答 (Ⅰ)证明:∵AB是直径,∴BC⊥AC,
∵CD⊥平面ABC,∴CD⊥BC,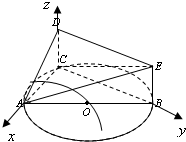
∵AC∩CD=C,∴BC⊥平面ACD.
∵CD∥BE,CD=BE,∴四边形BCDE是平行四边形,
则BC∥DE,∴DE⊥平面ACD.
∵DE?平面ADE,∴平面ADE⊥平面ACD;
(Ⅱ)解:如图所示,建立空间直角坐标系,则D(0,0,1),E(0,$2\sqrt{2}$,1),A($2\sqrt{2}$,0,0),
则$\overrightarrow{DE}=(0,2\sqrt{2},0)$,$\overrightarrow{DA}=(2\sqrt{2},0,-1)$,
设面DAE的法向量为$\overrightarrow{{n}_{1}}=(x,y,z)$,则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{DE}=2\sqrt{2}y=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{DA}=2\sqrt{2}x-z=0}\end{array}\right.$,
取x=1,得$\overrightarrow{{n}_{1}}=(1,0,2\sqrt{2})$,
由题意可知平面ABE的法向量为$\overrightarrow{{n}_{2}}=\overrightarrow{CO}=(\sqrt{2},\sqrt{2},0)$,
∴cos<$\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}$>=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}=\frac{\sqrt{2}}{2×3}=\frac{\sqrt{2}}{6}$.
可以判断<$\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}$>与二面角D-AE-B的平面角互补,
∴二面角D-AE-B的余弦值为-$\frac{\sqrt{2}}{6}$.
点评 本题考查平面与平面垂直的判定,考查空间想象能力和思维能力,训练了利用空间向量求二面角的大小,是中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当x>0且x≠1时,$lgx+\frac{1}{lgx}≥2$ | B. | 当x>0时,$\sqrt{x}+\frac{1}{{\sqrt{x}}}≥2$ | ||
| C. | 当x≥2时,$x+\frac{1}{x}≥2$ | D. | 当0<x≤2时,$x-\frac{1}{x}$无最大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
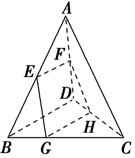 如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2,求证:
如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{{\sqrt{15}}}{2}$ | D. | $\frac{{\sqrt{19}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com