Question

3．已知函数f（x）=alnx+ax²+bx，（a，b∈R）．
（1）设a=1，f（x）在x=1处的切线过点（2，6），求b的值；
（2）设b=a²+2，求函数f（x）在区间[1，4]上的最大值；
（3）定义：一般的，设函数g（x）的定义域为D，若存在x₀∈D，使g（x₀）=x₀成立，则称x₀为函数g（x）的不动点．设a＞0，试问当函数f（x）有两个不同的不动点时，这两个不动点能否同时也是函数f（x）的极值点？

Answer 1

分析 （1）由题意a=1，f（x）在x=1处的切线过点（2，6），利用导数函数的几何性质求解b的值；
（2）b=a²+2，求函数f（x），求其导函数，讨论在区间[1，4]上的最大值；
（3）根据函数g（x）的不动点新定义，求其f（x）定义域，当a＞0时，g（x₀）=x₀讨论函数f（x）有两个不同的不动点；同时求函数f（x）的极值点，即可知道两个不动点能否同时也是函数f（x）的极值点．

解答 解：（1）对f（x）进行求导：f'（x）=$\frac{a}{x}$+2ax+b
当a=1时，f（x）=lnx+x²+bx，f'（x）=$\frac{1}{x}$+2x+b
当x=1时，f（1）=1+b，f'（1）=3+b
故切线方程为：y-（1+b）=（3+b）（x-1）
点（2，6）满足切线方程，故b=1．
（2）由题意，f（x）=alnx+ax²+（a²+2）x，x＞0
则：f'（x）=$\frac{a}{x}$+2ax+a²+2=$\frac{（ax+1）（2x+a）}{x}$
当a=0时，f（x）=2x，f'（x）=2＞0，f（x）在[1，4]上为增函数，故最大值为f（4）=8；
当a＞0时，f'（x）＞0，f（x）在x＞0上为增函数，故最大值为f（4）=4a²+（16+ln4）a+8；
当a＜0时，令f'（x）=0，则导函数有两个零点：x₁=-$\frac{1}{a}$，x₂=-$\frac{a}{2}$．
（i）当a＜$-\sqrt{2}$时，∵${x}_{1}=-\frac{1}{a}＜\frac{\sqrt{2}}{2}$，${x}_{2}=-\frac{a}{2}＞\frac{\sqrt{2}}{2}$∴x₁＜x₂，
  f（x）在（0，-$\frac{1}{a}$），（-$\frac{a}{2}$，+∞）上单调递减，在（-$\frac{1}{a}$，-$\frac{a}{2}$）上单调递增；
①当-$\frac{1}{a}$＜$\frac{\sqrt{2}}{2}$＜1＜4≤-$\frac{a}{2}$时，即a≤-8，此时最大值为f（4）=4a²+（16+ln4）a+8；
②当-$\frac{1}{a}$＜$\frac{\sqrt{2}}{2}$＜1＜-$\frac{a}{2}$≤4时，即-8≤a＜-2，此时最大值为f（-$\frac{a}{2}$）=aln（-$\frac{a}{2}$）-$\frac{1}{4}{a}^{3}$-a；
③当$-\frac{1}{a}$＜$\frac{\sqrt{2}}{2}$＜$-\frac{a}{2}$≤1＜4时，即-2≤a＜-$\sqrt{2}$，此时最大值为f（1）=a²+a+2；
（ii）当a=-$\sqrt{2}$时，${x}_{1}={x}_{2}=\frac{\sqrt{2}}{2}$，f'（x）≤0，f（x）在[1，4]上单调递减，最大值为f（1）=4-$\sqrt{2}$；
（iii）当-$\sqrt{2}$＜a＜0时，${x}_{1}=-\frac{1}{a}＞\frac{\sqrt{2}}{2}$，${x}_{2}=-\frac{a}{2}＜\frac{\sqrt{2}}{2}$∴x₁＞x₂
f（x）在（0，-$\frac{a}{2}$），（-$\frac{1}{a}$，+∞）上单调递减，（-$\frac{a}{2}$，-$\frac{1}{a}$）上单调递增；
①当$-\frac{a}{2}＜\frac{\sqrt{2}}{2}＜1＜4≤-\frac{1}{a}$时，即$-\frac{1}{4}$≤a＜0，最大值为f（4）=4a²+（16+ln4）a+8；
②当-$\frac{a}{2}$＜$\frac{\sqrt{2}}{2}$＜1＜-$\frac{1}{a}$≤4时，即-1＜a≤$-\frac{1}{4}$，最大值为f（-$\frac{1}{a}$）=aln（-$\frac{1}{a}$）-a-$\frac{1}{a}$；
③当-$\frac{a}{2}$＜$\frac{\sqrt{2}}{2}$＜-$\frac{1}{a}$≤1＜4时，即-$\sqrt{2}$＜a≤-1，最大值为f（1）=a²+a+2；
（3）由题意知：f（x）=$\left\{\begin{array}{l}{f（x）=x}\\{f'（x）=0}\end{array}\right.$⇒$\left\{\begin{array}{l}{alnx+a{x}^{2}+bx=x\\;①}\\{2a{x}^{2}+bx+a=0\\;②}\end{array}\right.$
由①②化简后：alnx-a-ax²=x⇒则说明 a（lnx-x²-1）=x 有两个根；
∵a＞0，x＞0∴$\frac{lnx-{x}^{2}-1}{x}$=$\frac{1}{a}$
即 y=$\frac{1}{a}$ 与 y=h（x）=$\frac{lnx-{x}^{2}-1}{x}$ 在（0，+∞）上有两个不同交点．
h'（x）=$\frac{2-{x}^{2}-lnx}{{x}^{2}}$，令F（x）=2-x²-lnx⇒F'（x）=-2x-$\frac{1}{x}$＜0；
∴F（x）在x＞0上单调递减；
∵F（1）＞0，F（$\frac{3}{2}$）＜0∴F（x）的零点为x₀∈（1，$\frac{3}{2}$），
故F（x₀）=0，即2-${x}_{0}^{2}$-lnx₀=0⇒lnx₀=2-${x}_{0}^{2}$  ③；
所以，h（x）在（0，x₀）单调递减，（x₀，+∞）上单调递增；
h（x₀）=$\frac{ln{x}_{0}-1-{x}_{0}^{2}}{{x}_{0}}$=$\frac{1-2{x}_{0}^{2}}{{x}_{0}}$=$\frac{1}{{x}_{0}}-2{x}_{0}$，h（x₀）∈（-$\frac{7}{3}$，-1）；
故h（x）的图形如右图：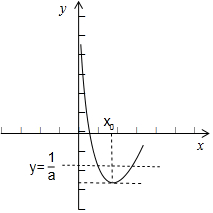
当$\frac{1}{a}$＜0时即a＜0，h（x）图形与y=$\frac{1}{a}$图形有两个交点，与题设a＞0
相互矛盾，故a不存在．

点评 本题考查了函数的导数的应用，同时考查了函数在闭区间上最值，属于中档题