
分析 (1)由$\frac{{{b^2}-{a^2}-{c^2}}}{ac}$=$\frac{{cos({A+C})}}{sinAcosA}$,利用余弦定理可得-2cosB=$\frac{-cosB}{sinAcosA}$,cosB≠0,化为:sinAcosA=$\frac{1}{2}$,与sin2A+cos2A=1联立基础即可得出..
(2)由余弦定理可得:2=b2+c2-2bccos45°,再利用基本不等式的性质即可得出.
解答 解:(1)∵$\frac{{{b^2}-{a^2}-{c^2}}}{ac}$=$\frac{{cos({A+C})}}{sinAcosA}$,∴-2cosB=$\frac{-cosB}{sinAcosA}$,cosB≠0,
化为:sinAcosA=$\frac{1}{2}$,又sin2A+cos2A=1,A为锐角,解得A=45°.
(2)由余弦定理可得:2=b2+c2-2bccos45°≥2bc-$\sqrt{2}$bc,可得bc≤2+$\sqrt{2}$,当且仅当b=c=$\sqrt{2+\sqrt{2}}$时取等号.
∴0<bc≤2+$\sqrt{2}$.
点评 本题考查了余弦定理、三角形的边角大小关系、基本不等式的性质、三角函数基本关系式,考查了推理能力与计算能力,属于中档题.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x≥2或x≤-2} | B. | {x|x≥-1或x≤2} | C. | {x|-1≤x≤2} | D. | {x|-2≤x≤-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,1) | C. | (1,2] | D. | [2.+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
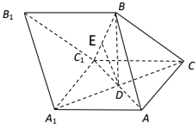 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
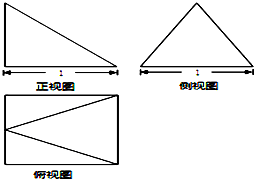
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com