
分析 (1)设公差为d,则$\left\{\begin{array}{l}{q+(6+d)=12}\\{6+d={q}^{2}}\end{array}\right.$,解得d,q即可得出.
(2)由(1)可知cn=3n-2λn,由数列{cn}是递增数列,可知cn<cn+1恒成立,代入化简即可得出.
解答 解:(1)设公差为d,则$\left\{\begin{array}{l}{q+(6+d)=12}\\{6+d={q}^{2}}\end{array}\right.$,解得d=q=3,
所以an=3+3(n-1)=3n,bn=3n-1;
(2)由(1)可知cn=3n-2λn,
由数列{cn}是递增数列,可知cn<cn+1恒成立,
即3n-2λn<3n+1-2λ(n+1)恒成立,即λ<3n恒成立,
显然,数列{3n}是递增数列,
∴当n=1时,3n取最小值3,
所以λ<3.
点评 本题考查了等差数列的通项公式与求和公式、数列递推关系、数列的单调性、不等式的解法,考查了推理能力与计算能力,属于中档题.


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
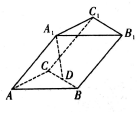 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | i | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3.5 | B. | 3.5 | C. | -4.5 | D. | 4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com