
| A. | $[{\frac{1}{e^2},\frac{1}{e}}]$ | B. | $[{\frac{1}{e^2},\frac{1}{e}})$ | C. | $[{\frac{2}{{3{e^2}}},\frac{1}{2e}}]$ | D. | $[{\frac{2}{{3{e^2}}},\frac{1}{2e}})$ |
分析 判断f(x)的单调性,作出f(x)与y=a(x+1)的图象,根据图象和整数解的个数判断a的范围.
解答 解:f′(x)=$\frac{1-x}{{e}^{x}}$,
∴当x<1时,f′(x)>0,当x>1时,f′(x)<0,
∴f(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减,
作出y=f(x)的函数图象如图所示: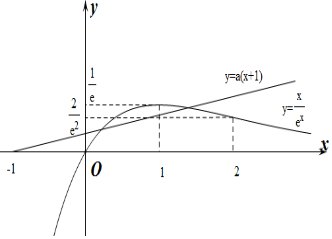
∵由f(x)-a(x+1)>0仅有一个整数解得f(x)>a(x+1)只有一整数解,
设g(x)=a(x+1),
由图象可知:当a≤0时,f(x)>g(x)在(0,+∞)上恒成立,不符合题意,
当a>0时,若f(x)>g(x)只有1个整数解,则此整数解必为1,
∴$\left\{\begin{array}{l}{f(1)>g(1)}\\{f(2)≤g(2)}\end{array}\right.$,即$\left\{\begin{array}{l}{\frac{1}{e}>2a}\\{\frac{2}{{e}^{2}}≤3a}\end{array}\right.$,解得$\frac{2}{3{e}^{2}}$≤a<$\frac{1}{2e}$.
故选D.
点评 本题考查了不等式与函数图象的关系,函数单调性的判断,属于中档题.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
| A类 | B类 | C类 | |
| 男生 | 5 | x | 5 |
| 女生 | y | 5 | 3 |
| 男生 | 女生 | 总计 | |
| 课余不参加体育锻炼 | |||
| 课余参加体育锻炼 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 用黑白两种颜色随机地染如图所示表格中6个格子,每个格子染一种颜色,则有64个不同的染色方法,出现从左至右数,不管数到哪个格子,总有黑色格子不少于白色格子的概率为$\frac{5}{16}$.
用黑白两种颜色随机地染如图所示表格中6个格子,每个格子染一种颜色,则有64个不同的染色方法,出现从左至右数,不管数到哪个格子,总有黑色格子不少于白色格子的概率为$\frac{5}{16}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com