
分析 (1)由条件利用正弦函数的单调性求得f(x)的单调递减区间.
(2)由x∈[0,$\frac{π}{2}$],利用正弦函数的定义域和值域,求得f(x)在x∈[0,$\frac{π}{2}$]内的值域.
解答 解:(1)对于函数f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),当2kπ+$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,k∈Z,
即kπ+$\frac{π}{8}$≤x≤kπ+$\frac{5π}{8}$,k∈Z时函数单调递增.
所以f(x)的单调递减区间为[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z.
(2)由x∈[0,$\frac{π}{2}$],知2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],从而sin(2x+$\frac{π}{4}$)∈[-$\frac{{\sqrt{2}}}{2}$,1],
故所求值域为[-1,$\sqrt{2}$].
点评 本题主要考查正弦函数的单调性、定义域和值域,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合计 | p | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制成如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取60名同学的试卷进行分析,则从成绩在[90,100]内的学生中抽取的人数为( )
某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制成如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取60名同学的试卷进行分析,则从成绩在[90,100]内的学生中抽取的人数为( )| A. | 24 | B. | 18 | C. | 15 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(理)试卷(解析版) 题型:选择题
函数 是定义在实数集
是定义在实数集 上的奇函数,且当
上的奇函数,且当 时,
时, 成立,若
成立,若 ,则
,则 大小关系( )
大小关系( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
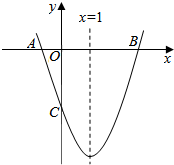 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com