
分析 AA的分配方案有2种,若A分配到的班级不再分配其他学生,若A分配到的班级再分配一名学生,若A分配到的班级再分配两名学生,根据分类分步计数原理可得.
解答 解:A的分配方案有2种,若A分配到的班级不再分配其他学生,则把其余四人分组后分配到另外两个班级,分配方法种数是(C43+$\frac{{C}_{4}^{2}{C}_{2}^{2}}{{A}_{2}^{2}}$)A22=14;
若A分配到的班级再分配一名学生,则把剩余的三名学生分组后分配到另外两个班级,分配方法种数是C41C31A22=24;
若A分配到的班级再分配两名学生,则剩余的两名学生就分配到另外的两个班级,分配方法种数是C42A22=12.故总数为2×(14+24+12)=100.
故答案为:100.
点评 本题考查计数原理的应用,解题注意优先分析排约束条件多的元素.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{e-\sqrt{{e}^{2}-1}}{e}$ | B. | $\frac{\sqrt{2{e}^{2}+1}-e}{e}$ | C. | $\frac{\sqrt{{e}^{2}+1}-e}{e}$ | D. | e+$\frac{1}{e}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (8,-6) | B. | (-6,1) | C. | (7,17) | D. | (-7,17) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n(n+2) | B. | $\frac{n}{2}$(2n+3) | C. | n(2n+3) | D. | $\frac{n}{2}$(2n+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
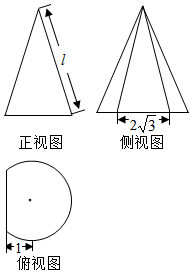 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | $\sqrt{2}+\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com