练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．函数f（x）=x-lnx的单调递减区间是（　　）
    A．（0，1）B．（0，+∞）C．（1，+∞）D．（-∞，0）∪（1，+∞）

    分析 求出函数的导数为y′，再解y'＜0得x的范围．结合函数的定义域，即可得到单调递减区间．

    解答 解：函数y=x-lnx的导数为y=1-$\frac{1}{x}$，
    令y′=1-$\frac{1}{x}$＜0，得x＜1
    ∴结合函数的定义域，得当x∈（0，1）时，函数为单调减函数．
    因此，函数y=x-lnx的单调递减区间是（0，1）
    故选：A．

    点评 本题给出含有对数的基本函数，求函数的减区间，着重考查了利用导数研究函数的单调性和函数的定义域等知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知向量$\overrightarrow{a}$=（k，3），$\overrightarrow{b}$=（1，4），$\overrightarrow{c}$=（2，1）且（3$\overrightarrow{a}$-2$\overrightarrow{b}$）⊥$\overrightarrow{c}$，则实数k=（　　）
    A．-$\frac{9}{2}$B．0C．3D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．定义在R上的可导函数f（x），其导数为f′（x），则“f′（x）为偶函数”是“f（x）为奇函数”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示．假设这辆汽车的里程表在汽车行驶这段路程前的读数为2000km，试建立行驶这段路程时汽车里程表读数s 与时间t 的函数解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

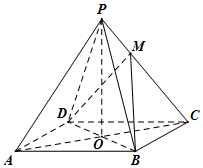    10．如图，已知四棱锥P-ABCD的底面是菱形，对角线AC，BD交于点O，OA=4，OB=3，OP=4，OP⊥底面ABCD，设点M满足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$（λ＞0）．
    （1）求当λ为何值时，使得PA∥平面BDM；
    （2）当λ=$\frac{1}{2}$时，求直线PA与平面BDM所成角的正弦值；
    （3）若二面角M-AB-C的大小为$\frac{π}{4}$，求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．函数f（x）=x2-2lnx的单调减区间是（　　）
    A．（0，1）B．（1，+∞）C．（-∞，-1）∪（0，1）D．（-1，0）∪（0，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．平面直角坐标系中，直线l的参数方程是$\left\{\begin{array}{l}{x=t}\\{y=\sqrt{3}t}\end{array}\right.$（t为参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐
    标系，已知曲线C的极坐标方程为4ρ2cos2θ-4ρsinθ-3=0．
    （I）求直线l的极坐标方程；
    （II）若直线l与曲线C相交于A、B两点，求|AB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．sin18°•sin78°-cos162°•cos78°=$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设a=ln2，b=log23，c=log3$\frac{1}{2}$，则a，b，c的大小关系是（　　）
    A．a＞c＞bB．b＞c＞aC．b＞a＞cD．c＞b＞a

    查看答案和解析>>

    同步练习册答案