
分析 (Ⅰ)通过构造函数,利用函数的导数,通过函数的单调性以及函数的最值推出结果.
(Ⅱ)直接利用数学归纳法的证明步骤,结合分析法以及(1)的结论证明即可.
解答 证明:(Ⅰ)设$f(x)=lnx+\frac{1}{x}-1$,
则$f'(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$.
所以当x>1时,f'(x)>0,f(x)为增函数;当0<x<1时,f'(x)<0,f(x)为减函数;
所以f(x)min=f(1)=0,
所以$lnx≥1-\frac{1}{x}$.…(4分)
(Ⅱ)(1)当n=1时,不等式左边为ln2,右边为$\frac{1}{2}=ln\sqrt{e}$,显然$ln2>ln\sqrt{e}$,所以左>右;
…(6分)
(2)假设n=k(k∈N+)时,有$ln(k+1)>\frac{1}{2}+\frac{1}{3}+…+\frac{1}{k+1}$,…(7分)
现欲证$ln(k+2)>\frac{1}{2}+\frac{1}{3}+…+\frac{1}{k+1}+\frac{1}{k+2}$,
只需证明$ln(k+1)<ln(k+2)-\frac{1}{k+2}$,只需证明$ln(\frac{k+2}{k+1})>\frac{1}{k+2}=1-\frac{k+1}{k+2}=1-\frac{1}{{\frac{k+2}{k+1}}}$,
由(Ⅰ)可得x≠1时,恒有$lnx>1-\frac{1}{x}$,因为$\frac{k+2}{k+1}≠1$,所以$ln(\frac{k+2}{k+1})>1-\frac{1}{{\frac{k+2}{k+1}}}$成立.
…(11分)
所以$ln(k+1+1)=ln(k+2)>\frac{1}{2}+\frac{1}{3}+…+\frac{1}{k+1}+\frac{1}{k+1+1}$
综合(1),(2)可得$ln(n+1)>\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n+1}$(n∈N+)成立.…(12分)
点评 本题考查反证法以及函数的导数的应用,数学归纳法的应用,考查逻辑推理能力以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}+\frac{3}{2}i$ | B. | 1 | C. | 2 | D. | $\frac{{\sqrt{10}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③都不能为系统抽样 | B. | ②④都不能为分层抽样 | ||
| C. | ①④都可能为系统抽样 | D. | ①③都可能为分层抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 废品率每增加1%,生铁成本增加258元 | |
| B. | 废品率每增加1%,生铁成本增加2元 | |
| C. | 废品率每增加1%,生铁成本每吨增加2元 | |
| D. | 废品率不变,生铁成本为256元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
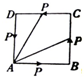 如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )
如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$-2 | D. | 3$\sqrt{2}$-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com