考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(1)利用导数得出切线的斜率即可得出f(x)在点(1,e)处的切线方程;
(2)令h(x)=f(x)-(
x
2+x+1)=e
x-
x
2-x-1,利用导数研究函数h(x)的单调性即可得出.
(3)利用作差法,再构造函数,令g(x)=x+2+(x-2)e
x(x>0),利用导数研究其单调性即可证明.
解答:
(1)解:f′(x)=e
x,则f'(1)=e,f(x)点(1,e)处的切线方程为:y-e=e(x-1),y=ex;
(2)证明:令
h(x)=f(x)-x2-x-1=ex-x2-x-1,x∈R,则h′(x)=e
x-x-1,h″(x)=e
x-1,且h(0)=0,h′(0)=0,h″(0)=0
因此,当x<0时,h″(x)<0,y=h′(x)单调递减;当x>0时,h″(x)>0,y=h′(x)单调递增.
所以y=h′(x)≥h′(0)=0,所以y=h(x)在R上单调递增,又h(0)=0,即函数h(x)有唯一零点x=0,
所以曲线y=f(x)与曲线
y=x2+x+1有唯一公共点(0,1);
(3)解:设a<b,
f(
)-
=
| (b-2+a) +(b-2+a)eb-a•ea |
| 2(b-a) |
,
令g(x)=x+2+(x-2)e
x(x>0),则g′(x)=1+(x-1)e
x.
g
′′(x)=xe
x>0,∴g′(x)在(0,+∞)上单调递增,且g′(0)=0,
∴g′(x)>0,∴g(x)在(0,+∞)上单调递增,而g(0)=0,∴在(0,+∞)上,g(x)>0.
∵当x>0时,g(x)=x+2+(x-2)•e
x>0,且a<b,∴
| (b-2+a) +(b-2+a)eb-a•ea |
| 2(b-a) |
>0,
即f(
)>
.
点评:本题综合考查了利用导数研究切线、单调性、方程得根的个数、比较两个实数的大小等基础知识,考查了分类讨论的思想方法、转化与化归思想方法,考查了推理能力和计算能力,属于中档题.



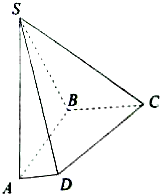 如图所示,在四棱锥S-ABCD中,底面ABCD是直角梯形,SA⊥平面ABCD,且AD∥BC,AB⊥AD,BC=2AD=2,AB=AS=
如图所示,在四棱锥S-ABCD中,底面ABCD是直角梯形,SA⊥平面ABCD,且AD∥BC,AB⊥AD,BC=2AD=2,AB=AS=