
ЗжЮі ЃЈ1ЃЉМЦЫуЃЈ$\overrightarrow{a}+\overrightarrow{b}$ЃЉ2ЃЌПЊЗНМДПЩЕУ|$\overrightarrow{a}+\overrightarrow{b}$|ЃЛ
ЃЈ2ЃЉгЩЃЈ$\overrightarrow{a}$+$\overrightarrow{b}$ЃЉ•$\overrightarrow{a}$=0ПЩЕУ$\overrightarrow{a}•\overrightarrow{b}$=-1ЃЌДњШыМаНЧЙЋЪНМЦЫуМДПЩЃЎ
НтД№ НтЃКЃЈ1ЃЉ$\overrightarrow{a}•\overrightarrow{b}$=1ЁС2ЁСcos60Ёу=1ЃЌ
ЁрЃЈ$\overrightarrow{a}+\overrightarrow{b}$ЃЉ2=${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=1+2+4=7ЃЌ
Ёр|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{7}$ЃЎ
ЃЈ2ЃЉШєЃЈ$\overrightarrow{a}$+$\overrightarrow{b}$ЃЉЁЭ$\overrightarrow{a}$ЃЌдђЃЈ$\overrightarrow{a}$+$\overrightarrow{b}$ЃЉ•$\overrightarrow{a}$=${\overrightarrow{a}}^{2}$+$\overrightarrow{a}•\overrightarrow{b}$=0ЃЌ
Ёр$\overrightarrow{a}•\overrightarrow{b}$=-${\overrightarrow{a}}^{2}$=-1ЃЌ
ЁрcosЃМ$\overrightarrow{a}ЃЌ\overrightarrow{b}$ЃО=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=-$\frac{1}{2}$ЃЌ
Ёп0ЁуЁмЃМ$\overrightarrow{a}ЃЌ\overrightarrow{b}$ЃОЁм180Ёу
Ёр$\overrightarrow{a}$гы$\overrightarrow{b}$ЕФМаНЧЮЊ120ЁуЃЎ
ЕуЦР БОЬтПМВщСЫЦНУцЯђСПЕФЪ§СПЛ§ЙЋЪНЃЌМаНЧгыФЃГЄМЦЫуЃЌЪєгкжаЕЕЬтЃЎ


 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ злКЯздВтЯЕСаД№АИ
злКЯздВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | {-$\frac{4}{3}$ЃЌ$\frac{2}{3}$} | BЃЎ | {$\frac{4}{3}$ЃЌ-$\frac{2}{3}$} | CЃЎ | {-$\frac{4}{3}$ЃЌ$\frac{2}{3}$ЃЌ$\frac{4}{3}$} | DЃЎ | {-$\frac{4}{3}$ЃЌ-$\frac{2}{3}$ЃЌ$\frac{2}{3}$} |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
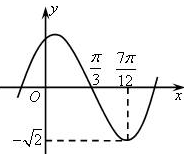 вбжЊКЏЪ§y=AsinЃЈІиx+ІеЃЉЃЈAЃО0ЃЌІиЃО0ЃЌ|Іе|ЃМ$\frac{Іа}{2}$ЃЉЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌдђКЏЪ§ЕФНтЮіЪНЮЊy=$\sqrt{2}$sinЃЈ2x+$\frac{Іа}{3}$ЃЉЃЎ
вбжЊКЏЪ§y=AsinЃЈІиx+ІеЃЉЃЈAЃО0ЃЌІиЃО0ЃЌ|Іе|ЃМ$\frac{Іа}{2}$ЃЉЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌдђКЏЪ§ЕФНтЮіЪНЮЊy=$\sqrt{2}$sinЃЈ2x+$\frac{Іа}{3}$ЃЉЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com