
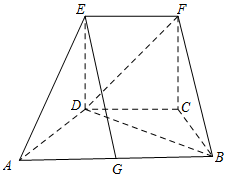
 如图所示的几何体中,四边形ABCD为等腰梯形,AB∥CD,AB=2AD=2,∠DAB=60°,四边形CDEF为正方形,平面CDEF⊥平面ABCD.
如图所示的几何体中,四边形ABCD为等腰梯形,AB∥CD,AB=2AD=2,∠DAB=60°,四边形CDEF为正方形,平面CDEF⊥平面ABCD.分析 (I)求出CD=1,证明四边形EFBG是平行四边形得出EG∥BF即可得出EG∥平面BDF;
(II)建立空间坐标系,求出平面BDF的法向量$\overrightarrow{n}$和$\overrightarrow{AE}$的坐标,则直线AE与平面BDF所成角的正弦值为|cos<$\overrightarrow{AE},\overrightarrow{n}$>|;
(III)假设存在H点满足条件,求出平面HAD的法向量$\overrightarrow{m}$,令$\overrightarrow{m}•\overrightarrow{n}$=0,根据方程是否有解得出结论.
解答 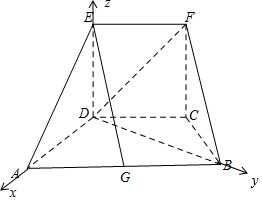 (I)证明:∵四边形ABCD为等腰梯形,AB∥CD,AB=2AD=2,∠DAB=60°,
(I)证明:∵四边形ABCD为等腰梯形,AB∥CD,AB=2AD=2,∠DAB=60°,
∴CD=AB-2ADcos60°=1,即CD=$\frac{1}{2}$AB.
∵CD$\stackrel{∥}{=}$EF,CD$\stackrel{∥}{=}$$\frac{1}{2}$AB,又BG=$\frac{1}{2}$AB,
∴EF$\stackrel{∥}{=}$$\frac{1}{2}$BG,
∴四边形EFBG是平行四边形,
∴EG∥BF,
又EG?平面BDF,BF?平面BDF,
∴EG∥平面BDF
(II)解:∵AD=1,AB=2,∠DAB=60°,∴BD=$\sqrt{1+4-2×2×1×cos60°}$=$\sqrt{3}$,
∴AD2+BD2=AB2,∴AD⊥BD.
∵平面CDEF⊥平面ABCD,平面CDEF∩平面ABCD=CD,DE⊥CD,
∴DE⊥平面ABCD.
以D为原点,以直线DA,DC,DE为坐标轴建立空间直角坐标系D-xyz,如图所示:
则A(1,0,0),E(0,0,1),B(0,$\sqrt{3}$,0),D(0,0,0),F(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,1)
∴$\overrightarrow{AE}$=(-1,0,1),$\overrightarrow{DB}$=(0,$\sqrt{3}$,0),$\overrightarrow{DF}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,1),
设平面BDF的法向量为$\overrightarrow{n}$=(x,y,z),则$\overrightarrow{n}•\overrightarrow{DB}=0$,$\overrightarrow{n}•\overrightarrow{DF}$=0,
∴$\left\{\begin{array}{l}{\sqrt{3}y=0}\\{-\frac{1}{2}x+\frac{\sqrt{3}}{2}y+z=0}\end{array}\right.$,令z=1得$\overrightarrow{n}$=(2,0,1),
∴cos<$\overrightarrow{AE},\overrightarrow{n}$>=$\frac{\overrightarrow{AE}•\overrightarrow{n}}{|\overrightarrow{AE}||\overrightarrow{n}|}$=$\frac{-1}{\sqrt{2}×\sqrt{5}}$=-$\frac{\sqrt{10}}{10}$,
设直线AE与平面BDF所成角为θ,则sinθ=|cos<$\overrightarrow{AE},\overrightarrow{n}$>|=$\frac{\sqrt{10}}{10}$.
(3)解:设H(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,h),(0≤h≤1)
当h=0时,显然平面BDF与平面HAD不垂直,
则$\overrightarrow{DH}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,h),$\overrightarrow{DA}$=(1,0,0),
设平面HAD的法向量为$\overrightarrow{m}$=(x,y,z),则$\overrightarrow{m}•\overrightarrow{DH}=0$,$\overrightarrow{m}•\overrightarrow{DA}=0$,
∴$\left\{\begin{array}{l}{-\frac{1}{2}x+\frac{\sqrt{3}}{2}y+hz=0}\\{x=0}\end{array}\right.$,令y=$\sqrt{3}$得$\overrightarrow{m}$=(0,$\sqrt{3}$,-$\frac{3}{2h}$).
假设存在点H,使得平面BDF⊥平面HAD,则$\overrightarrow{m}⊥\overrightarrow{n}$,
∴$\overrightarrow{m}•\overrightarrow{n}$=-$\frac{3}{2h}$=0,方程无解.
∴线段FC上不存在点H,使平面BDF⊥平面HAD.
点评 本题考查了线面平行的判定,空间向量与空间角,空间位置的关系,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
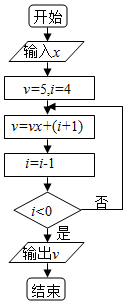 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )| A. | 129 | B. | 144 | C. | 258 | D. | 289 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. | 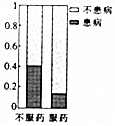 | D. | 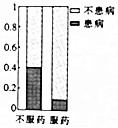 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | $2\sqrt{5}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com