
分析 利用反三角函数的定义,两角和差的三角公式,求得要求式子的值.
解答 解:(1)sin[arcsin$\frac{1}{2}$+arccos(-$\frac{\sqrt{3}}{2}$)]=sin($\frac{π}{6}$+$\frac{5π}{6}$)=sinπ=0;
(2)sin(arccos$\frac{12}{13}$)=$\sqrt{{1-cos}^{2}(arccos\frac{12}{13})}$=$\sqrt{1-\frac{144}{169}}$=$\frac{5}{13}$;
(3)sin(arccos(-$\frac{12}{13}$)=$\sqrt{{1-cos}^{2}[arccos(-\frac{12}{13})]}$=$\sqrt{1-\frac{144}{169}}$=$\frac{5}{13}$;
(4)sin($\frac{π}{6}$-arccos$\frac{4}{5}$)=sin$\frac{π}{6}$cos(arccos$\frac{4}{5}$)-cos$\frac{π}{6}$sin(arccos$\frac{4}{5}$)=$\frac{1}{2}•\frac{4}{5}$-$\frac{\sqrt{3}}{2}$•$\frac{3}{5}$=$\frac{4-3\sqrt{3}}{10}$;
(5)sin(2arccos$\frac{4}{5}$)=2sin(arccos$\frac{4}{5}$)cos(arccos$\frac{4}{5}$)=2•$\frac{3}{5}$•$\frac{4}{5}$=$\frac{24}{25}$.
点评 本题主要考查反三角函数的定义,两角和差的三角公式的应用,属于基础题.


 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:解答题
 在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机与不晕机的人数如图所示.
在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机与不晕机的人数如图所示. | P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 晕机 | 不晕机 | 合计 | |
| 女 | 10 | 20 | 30 |
| 男 | 10 | 70 | 80 |
| 合计 | 20 | 90 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $-\frac{1}{6}$ | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
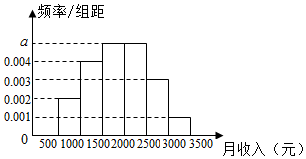 统计局就某地居民的月收入情况调查了10000人,并根据所得数据画出了样本频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[500,1000)元.
统计局就某地居民的月收入情况调查了10000人,并根据所得数据画出了样本频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[500,1000)元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com