
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,2) | C. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
分析 由f′(x)<$\frac{1}{4}$,构造辅助函数g(x)=f(x)-$\frac{1}{4}$x,求导,利用导数判断函数单调递减,根据f(2)=1,求得g(2)=$\frac{1}{2}$,根据f(x2)<$\frac{{x}^{2}}{4}$+$\frac{1}{2}$,将其转换成g(x2)<g(2),根据函数单调性即可求得不等的解集.
解答 解:f′(x)<$\frac{1}{4}$(x∈R),
f′(x)-$\frac{1}{4}$<0,
设g(x)=f(x)-$\frac{1}{4}$x,
g′(x)=f′(x)-$\frac{1}{4}$<0,
∴g(x)是R上的减函数,g(2)=g(2)-$\frac{2}{4}$=$\frac{1}{2}$,
∴f(x2)<$\frac{{x}^{2}}{4}$+$\frac{1}{2}$,
g(x2)=f(x2)-$\frac{{x}^{2}}{4}$<$\frac{1}{2}$=g(2),
∴x2>2,
解得:x>$\sqrt{2}$或x<-$\sqrt{2}$,
∴原不等式的解集为(-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞).
故答案选:C.
点评 本题考查抽象不等式求解,关键是利用函数的单调性,根据已知条件和所要解的不等式,找到合适的函数作载体是关键,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
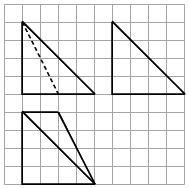 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱与最短的棱所成角的余弦值是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱与最短的棱所成角的余弦值是( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | -1 | 0 | 1 | 2 | 3 |
| P | 0.16 | $\frac{a}{10}$ | a2 | $\frac{a}{5}$ | 0.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com