
【题目】设![]() 是正整数,集合
是正整数,集合![]() 是数集
是数集![]() 的一个子集,且
的一个子集,且![]() 中任意两个数的差不等于4或7.若
中任意两个数的差不等于4或7.若![]() 的元素个数的最大值记为
的元素个数的最大值记为![]() (如
(如![]() ,
,![]() ),试求
),试求![]() .
.
【答案】![]()
【解析】
易知1、4、6、7、9这五个数中的任意两个数的差都不是4或7,各加上11得到12、15、17、18、20,显然也是这样的数,且各与前五个数中的任意一个数的差也不是4或7.由此类推知,对于每个确定的正整数![]() ,每连续11个数中可取五个数,余下的
,每连续11个数中可取五个数,余下的![]() 个数中取
个数中取![]() 个数,一起组成集合
个数,一起组成集合![]() (
(![]() 表示不超过实数
表示不超过实数![]() 的最大整数).
的最大整数).
下面证明:![]() 中不可能包含更多的数.
中不可能包含更多的数.
倘若不然,则上述![]() 中前各11数组中至少有一组可以从中取六个数,使得任意两个数之差都不是4或7.
中前各11数组中至少有一组可以从中取六个数,使得任意两个数之差都不是4或7.
不妨考虑1,2,,11这组数,把它们分成五个小组:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中,至少要求有一组要取出两个数.显然,前四组中每组的两个数不能同取,最多一组取一个数,因此,只能在第五组
,其中,至少要求有一组要取出两个数.显然,前四组中每组的两个数不能同取,最多一组取一个数,因此,只能在第五组![]() 中取4、7.
中取4、7.
于是,![]() 中只能取1,
中只能取1,![]() 中只能取9,
中只能取9,![]() 中只能取6.
中只能取6.
这样,![]() 中3、10这两个数都不能取,从而知不可能取得第六个数.故
中3、10这两个数都不能取,从而知不可能取得第六个数.故
![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,如
时,如![]() ,可考虑余下1,2,…,8这八个数,把它们分成四个组:
,可考虑余下1,2,…,8这八个数,把它们分成四个组:
![]() ,
,![]() ,
,![]() ,
,![]() ,每组取一个共4个,即
,每组取一个共4个,即![]() ;
;
当![]() 时,如
时,如![]() ,可考虑余下1,2,…,9这九个数,把它们分成五个组:
,可考虑余下1,2,…,9这九个数,把它们分成五个组:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,可取1、3、4、6、9这五个数,
,可取1、3、4、6、9这五个数,![]() .
.
因为![]() ,所以,
,所以,
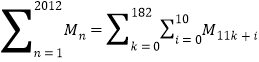
![]()
![]()
![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
周一 | 无雨 | 无雨 | 有雨 | 有雨 |
周二 | 无雨 | 有雨 | 无雨 | 有雨 |
收益 |
|
|
|
|
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为![]() 万元;有雨时,收益为
万元;有雨时,收益为![]() 万元.额外聘请工人的成本为
万元.额外聘请工人的成本为![]() 万元.
万元.
已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为![]() 万元的概率为
万元的概率为![]() .
.
(Ⅰ)若不额外聘请工人,写出基地收益![]() 的分布列及基地的预期收益;
的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市政府为做好![]() 会议接待服务工作,对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测,只有两轮都合格才能进行销售,否则不能销售.已知该海产品第一轮检测不合格的概率为
会议接待服务工作,对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测,只有两轮都合格才能进行销售,否则不能销售.已知该海产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.
(1)求该海产品不能销售的概率.
(2)如果该海产品可以销售,则每件产品可获利40元;如果该海产品不能销售,则每件产品亏损80元(即获利-80元).已知一箱中有该海产品4件,记一箱该海产品获利![]() 元,求
元,求![]() 的分布列,并求出数学期望
的分布列,并求出数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的
上每一点的横坐标保持不变,纵坐标变为原来的![]() ,得曲线
,得曲线![]() .
.
(1)求出![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设
轴正半轴为极轴建立极坐标系,设![]() 是曲线
是曲线![]() 上的一个动点,求点
上的一个动点,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某外语学校的一个社团有7名同学,其中2人只会法语,2人只会英语,3人既会法语又会英语,现选派3人到法国的学校交流访问.求:
(1)在选派的3人中恰有2人会法语的概率;
(2)求在选派的3人中既会法语又会英语的人数![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级学生会主席团有共有![]() 名同学组成,其中有
名同学组成,其中有![]() 名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )
名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列![]() 中,已知公差
中,已知公差![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)求![]() .
.
【答案】(1)![]() ;(2)100
;(2)100
【解析】试题分析:(1)根据题意![]() ,
, ![]() ,
, ![]() 成等比数列得
成等比数列得![]() 得
得![]() 求出d即可得通项公式;(2)求项的绝对前n项和,首先分清数列有多少项正数项和负数项,然后正数项绝对值数值不变,负数项绝对值要变号,从而得
求出d即可得通项公式;(2)求项的绝对前n项和,首先分清数列有多少项正数项和负数项,然后正数项绝对值数值不变,负数项绝对值要变号,从而得![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,∴
,∴![]()
![]()
![]()
![]() 计算 即可得出结论
计算 即可得出结论
解析:(1)由题意可得,则![]() ,
, ![]() ,
,
![]() ,即
,即![]() ,
,
化简得![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
(2)由(1)得![]() 时,
时,
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() .
.
∴![]() .
.
点睛:对于数列第一问首先要熟悉等差和等比通项公式及其性质即可轻松解决,对于第二问前n项的绝对值的和问题,首先要找到数列由多少正数项和负数项,进而找到绝对值所影响的项,然后在求解即可得结论
【题型】解答题
【结束】
18
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15-65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
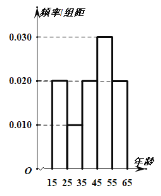
(1)由以上统计数据填2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]() .
.
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动、现从这8人中随机抽2人.记抽到45岁以上的人数为X,求随机变量X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com