
| A. | $\frac{2}{3}$ | B. | 2 | C. | $\frac{26}{3}$ | D. | $\frac{14}{3}$ |
分析 由题意可得f(x)的图象关于点($\frac{π}{4}$,0)对称,$\frac{π}{4}ω$-$\frac{π}{6}$=kπ,k∈Z.且$\frac{2π}{ω}$<$\frac{π}{2}$<$\frac{3}{2}$•$\frac{2π}{ω}$,求得6>ω>4,结合所给的选项,得出结论.
解答 解:∵函数f(x)=sin(ωx-$\frac{π}{6}$)(ω>0),f(0)=-f($\frac{π}{2}$),即f(0)+f($\frac{π}{2}$)=0,
故f(x)的图象关于点($\frac{π}{4}$,0)对称,故sin($\frac{π}{4}ω$-$\frac{π}{6}$)=0,故有$\frac{π}{4}ω$-$\frac{π}{6}$=kπ,k∈Z ①.
∵f(x)在(0,$\frac{π}{2}$)上有且仅有三个零点,故有$\frac{2π}{ω}$<$\frac{π}{2}$<$\frac{3}{2}$•$\frac{2π}{ω}$,∴6>ω>4 ②.
综合①②,结合所给的选项,可得ω=$\frac{14}{3}$,
故选:D.
点评 本题主要考查正弦函数的图象的对称性,正弦函数的周期性,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
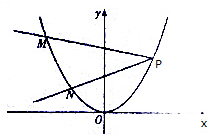 如图,点P(x0,$\frac{p}{2}$)(x0>0)在抛物线x2=2py(p>0)上.过P的直线PM,PN分别与抛物线交于点M(x1,y1)和N(x2,y2).
如图,点P(x0,$\frac{p}{2}$)(x0>0)在抛物线x2=2py(p>0)上.过P的直线PM,PN分别与抛物线交于点M(x1,y1)和N(x2,y2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com