
分析 (Ⅰ)由题意可知b=1,e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,即可求得a的值,求得椭圆方程;
(Ⅱ)将直线方程代入椭圆方程,利用韦达定理及弦长公式求得丨AC丨及丨MN丨,丨BN丨2=$\frac{1}{4}$丨AC丨2+丨MN丨2=$\frac{5}{2}$,即可求得B,N两点间距离是否为定值.
解答 解:(Ⅰ)由题意可知:椭圆的焦点在x轴上,过点(0,1),则b=1,
由椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,则a=2,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)设A(x1,y1),B(x2,y2),线段中点M(x0,y0),
则$\left\{\begin{array}{l}{y=\frac{1}{2}x+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,整理得:x2+2mx+2m2-2=0,
由△=(2m)2-4(2m2-2)=8-4m2>0,解得:-$\sqrt{2}$<m<$\sqrt{2}$,
则x1+x2=-2m,x1x2=2m2-2,则M(-m,$\frac{1}{2}$m),
丨AC丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+(\frac{1}{2})^{2}}$•$\sqrt{4{m}^{2}-4×(2{m}^{2}-2)}$=$\sqrt{10-5{m}^{2}}$
由l与x轴的交点N(-2m,0),
则丨MN丨=$\sqrt{(-m+2m)^{2}+(\frac{1}{2}m)^{2}}$=$\sqrt{\frac{5}{4}{m}^{2}}$,
∴丨BN丨2=丨BM丨2+丨MN丨2=$\frac{1}{4}$丨AC丨2+丨MN丨2=$\frac{5}{2}$,
∴B,N两点间距离是否为定值$\frac{\sqrt{10}}{2}$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,弦长公式及中点坐标公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 12 | C. | 24 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
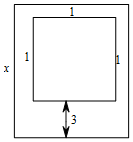 某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?
某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
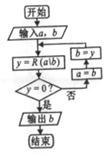 我国古代数学名著《九章算术》中的更相减损术的算法思路与右图类似.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为266,63,则输出的b的值为( )
我国古代数学名著《九章算术》中的更相减损术的算法思路与右图类似.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为266,63,则输出的b的值为( )| A. | 1 | B. | 3 | C. | 7 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com