
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| a |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |


科目:高中数学 来源: 题型:
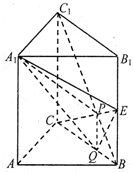 如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,E是BB1的中点,且CE交BC1于点P,点Q在线段BC上,CQ=2QB.
如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,E是BB1的中点,且CE交BC1于点P,点Q在线段BC上,CQ=2QB.查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| C |
| 2 |
| n |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 性别 中国政府是否 需要在钓鱼岛和其他争议 问题上持续对日强硬 |
男 | 女 |
| 需要 | 50 | 250 |
| 不需要 | 100 | 150 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
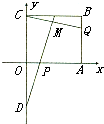 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,|OC|=
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,|OC|=| 3 |
| OP |
| OA |
| AQ |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com