
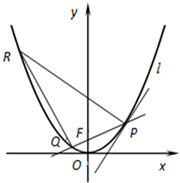
 如图,点F是抛物线C:x2=2y的焦点,点P(x1,y1)为抛物线上的动点(P在第一象限),直线PF交抛物线C于另一点Q,直线l与抛物线C相切于点P.过点P作直线l的垂线交抛物线C于点R.
如图,点F是抛物线C:x2=2y的焦点,点P(x1,y1)为抛物线上的动点(P在第一象限),直线PF交抛物线C于另一点Q,直线l与抛物线C相切于点P.过点P作直线l的垂线交抛物线C于点R.分析 (1)首先设出直线L的方程,联立方程组消元根据△=0,求出k的值即可;
(2)设出直线PF方程,与抛物线联立方程组求出PR直线方程,从而就出R点坐标;再根据点到直线的距离求出三角形高表达式,结合基本不等式来求出三角形面积最小值;
解答 解:(1)设L的斜率为k,则L的方程为:
y=k(x-x1)+$\frac{{x}_{1}^{2}}{2}$,
联立方程$\left\{\begin{array}{l}{{x}^{2}=2y}\\{y=k(x-{x}_{1})+\frac{{x}_{1}^{2}}{2}}\end{array}\right.$,消元化简得:
${x}^{2}-2kx+2k{x}_{1}-{x}_{1}^{2}=0$
因为直线L与抛物线相切,则由△=$4{k}^{2}-8k{x}_{1}+4{x}_{1}^{2}=0$,
可得k=x1
所以直线L的方程为y=${x}_{1}x-\frac{{x}_{1}^{2}}{2}$;
(2)设直线PF的方程为y=kx+$\frac{1}{2}$,
联立方程组$\left\{\begin{array}{l}{y=kx+\frac{1}{2}}\\{{x}^{2}=2y}\end{array}\right.$,消元化简得x2-2kx-1=0,又设Q(x2,$\frac{{x}_{2}^{2}}{2}$),则由根与系数的关系得:
x1+x2=2k,x1x2=-1;
直线PR的方程为y=$-\frac{x}{{x}_{1}}+\frac{{x}_{1}^{2}}{2}+1$,与x2=2y联立方程组,解得点R($-\frac{2+{x}_{1}^{2}}{{x}_{1}}$,$\frac{(2+{x}_{1}^{2})^{2}}{2{x}_{1}^{2}}$);
又因为k=$\frac{\frac{1}{2}{x}_{1}^{2}-\frac{1}{2}}{{x}_{1}}$=$\frac{{x}_{1}^{2}-1}{2{x}_{1}}$,所以k2+1=$(\frac{{x}_{1}^{2}+1}{2{x}_{1}})^{2}$;
则点R到直线PQ的距离为:
d=$\frac{|-\frac{k}{{x}_{1}}(2+{x}_{1}^{2})-\frac{1}{2{x}_{1}^{2}}(2+{x}_{1}^{2})^{2}+\frac{1}{2}|}{\sqrt{{k}^{2}+1}}$=$\frac{1}{\sqrt{{k}^{2}+1}}({x}_{1}+\frac{1}{{x}_{1}})^{2}$;
又因为|PQ|=|PF|+|QF|=2k2+2,
所以△PQR面积为:
S=$\frac{1}{2}$|PQ|d=$\sqrt{{k}^{2}+1}$$({x}_{1}+\frac{1}{{x}_{1}})^{2}$=$\frac{1}{2}$$({x}_{1}+\frac{1}{{x}_{1}})^{3}$≥$\frac{1}{2}$$(2\sqrt{{x}_{1}•\frac{1}{{x}_{1}}})^{3}$=4;
当且仅当x1=1即k=0时,取等号,所以△PQR面积的最小值为4.
点评 本题主要考查直线与抛物线的相对位置关系等问题,探索构造三角形面积最值,属较难题.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 15 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
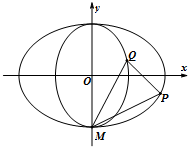 如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.
如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
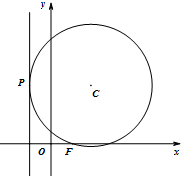 如图,动圆C过点F(1,0),且与直线x=-1相切于点P.
如图,动圆C过点F(1,0),且与直线x=-1相切于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{2}$ | B. | 2π | C. | 6π | D. | $\sqrt{6}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (-2,0) | C. | (0,4) | D. | (-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,0) | C. | (-∞,1) | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com