
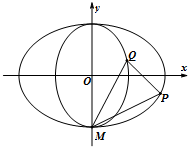
 如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.
如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.分析 (Ⅰ)由中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$,可求得椭圆T1与椭圆T2的标准方程;
(Ⅱ)联立直线与椭圆方程,求出P,Q的坐标,进而得到直线方程,可得直线PQ过定点(0,$\sqrt{2}$).
解答 解:(Ⅰ)∵椭圆T1与T2的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
∴$\frac{\sqrt{2}}{2}$a=b=c
∵焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),
故椭圆T1的b=c=$\sqrt{2}$,a=2,
椭圆T2的b=c=1,a=$\sqrt{2}$,
故椭圆T1与椭圆T2的标准方程分别为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(Ⅱ)直线MP的方程为$y=kx-\sqrt{2}$,
联立椭圆方程得:$\left\{\begin{array}{l}\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1\\ y=kx-\sqrt{2}\end{array}\right.$,
消去y得$(2{k}^{2}+1){x}^{2}-4\sqrt{2}kx=0$,则P点的横坐标为$\frac{4\sqrt{2}k}{2{k}^{2}+1}$,
则点P的坐标为($\frac{4\sqrt{2}k}{2{k}^{2}+1}$,$\frac{2\sqrt{2}{k}^{2}-\sqrt{2}}{2{k}^{2}+1}$)
同理可得点Q的坐标为:($\frac{4\sqrt{2}k}{8{k}^{2}+1}$,$\frac{8\sqrt{2}{k}^{2}-\sqrt{2}}{8{k}^{2}+1}$),
故直线PQ的斜率kPQ=$\frac{\frac{8\sqrt{2}{k}^{2}-\sqrt{2}}{8{k}^{2}+1}-\frac{2\sqrt{2}{k}^{2}-\sqrt{2}}{2{k}^{2}+1}}{\frac{4\sqrt{2}k}{8{k}^{2}+1}-\frac{4\sqrt{2}k}{2{k}^{2}+1}}$=-$\frac{1}{2k}$,
则直线PQ的方程为:y-$\frac{2\sqrt{2}{k}^{2}-\sqrt{2}}{2{k}^{2}+1}$=-$\frac{1}{2k}$(x-$\frac{4\sqrt{2}k}{2{k}^{2}+1}$),
即y=-$\frac{1}{2k}$x+$\sqrt{2}$,
即当x=0时,y=$\sqrt{2}$,
故直线PQ过定点(0,$\sqrt{2}$).
点评 本题考查的知识点是椭圆的标准方程,直线与圆锥曲线的关系,直线的方程,难度中档.


科目:高中数学 来源: 题型:解答题
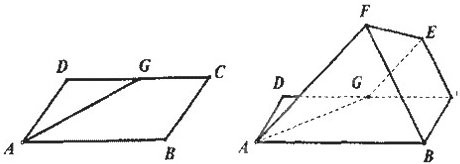
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
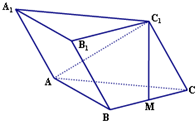 如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.
如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
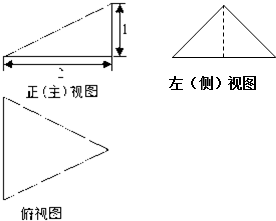
| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
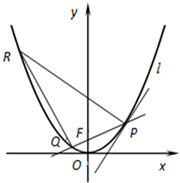 如图,点F是抛物线C:x2=2y的焦点,点P(x1,y1)为抛物线上的动点(P在第一象限),直线PF交抛物线C于另一点Q,直线l与抛物线C相切于点P.过点P作直线l的垂线交抛物线C于点R.
如图,点F是抛物线C:x2=2y的焦点,点P(x1,y1)为抛物线上的动点(P在第一象限),直线PF交抛物线C于另一点Q,直线l与抛物线C相切于点P.过点P作直线l的垂线交抛物线C于点R.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无穷多个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com