
【题目】如图,![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,离心率为
,离心率为![]() ,双曲线
,双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,已知
,已知![]() ,
,![]() .
.
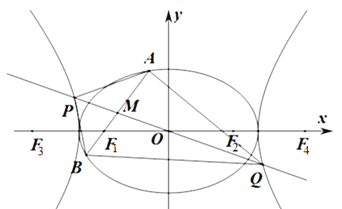
(1)求![]() ,
,![]() 的方程;
的方程;
(2)过![]() 作
作![]() 的不垂直于
的不垂直于![]() 轴的弦
轴的弦![]() ,
,![]() 为弦
为弦![]() 的中点,当直线
的中点,当直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点时,求四边形
两点时,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 可推出
可推出![]() ,从而
,从而![]() ,
,![]() ,因此
,因此![]() ,推出
,推出![]() ,
,![]() ,从而得到
,从而得到![]() 的方程;
的方程;
(2)设直线![]() 的方程为
的方程为![]() ,联立
,联立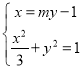 ,利用韦达定理和中点坐标公式求出
,利用韦达定理和中点坐标公式求出![]() ,从而得到直线
,从而得到直线![]() 的方程为
的方程为![]() ,再联立
,再联立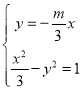 ,由韦达定理和弦长公式求出
,由韦达定理和弦长公式求出![]() ,再利用点到直线的距离公式求出
,再利用点到直线的距离公式求出![]() 到直线
到直线![]() 的距离以及
的距离以及![]() 到直线
到直线![]() 的距离,进而得到四边形
的距离,进而得到四边形![]() 的面积的最小值.
的面积的最小值.
(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 的方程为
的方程为![]() ,
,![]() 的方程为
的方程为![]() .
.
(2)依题意,直线![]() 的方程可设为
的方程可设为![]() ,设
,设![]() ,
,![]() ,
,
由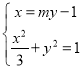 消去
消去![]() 可得
可得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 中点坐标为
中点坐标为![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,
,
由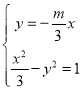 消去
消去![]() ,可得
,可得![]() ,
,
∴![]() 且
且![]() ,
,![]() ,
,
∴![]() ,
,
设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() 到直线
到直线![]() 的距离也为
的距离也为![]() ,
,
∴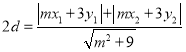 ,
,
∵![]() ,
,
∴ ,
,
又∵ ,
,
∴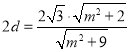 ,
,
∴四边形![]() 的面积
的面积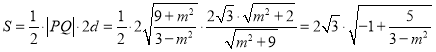 ,
,
∴当![]() 时,
时,![]() 取得最小值,且
取得最小值,且![]() ,即四边形
,即四边形![]() 面积的最小值为
面积的最小值为![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,正视图为等腰直角三角形,俯视图中虚线平分矩形的面积,则该几何体的体积为_____,其外接球的表面积为______.
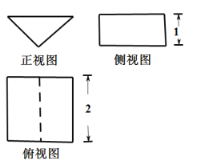
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() ,点
,点![]() 均在圆
均在圆![]() 上,且
上,且![]() ,过点
,过点![]() 作
作![]() 的平行线分别交
的平行线分别交![]() ,
,![]() 于
于![]() 两点.
两点.
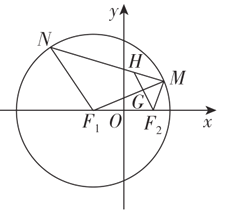
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点.问是否存在常数
两点.问是否存在常数![]() ,使得
,使得![]() 点为定值?若存在,求出
点为定值?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重. 大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如表所示的列联表:已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为![]() .
.
(1)请将列联表补充完整;
患心肺 疾病 | 不患心 肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
(2)是否有97.5%的把握认为患心肺疾病与性别有关?说明你的理由;
(3)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列以及数学期望.下面的临界值表供参考:
的分布列以及数学期望.下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点A
过点A![]() ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(Ⅰ)求椭圆C的方程;
(Ⅱ)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有250人参与学习先修课程.
(Ⅰ)这两年学校共培养出优等生150人,根据下图等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系?
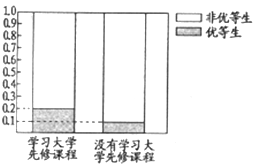
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | 250 | ||
没有学习大学先修课程 | |||
总计 | 150 |
(Ⅱ)某班有5名优等生,其中有2名参加了大学生先修课程的学习,在这5名优等生中任选3人进行测试,求这3人中至少有1名参加了大学先修课程学习的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com