
分析 根据集合与集合中间的关系即可判断.
解答 解:(1)集合A={1,2,3,4,5},M={x|x∈A},
当集合M的元素有1个,2个,3个,4个,5个,其子集的个数为21,22,23,24,25
(2)集合N满足{4,5}?N⊆M,根据条件知,4,5都是集合N的元素,并且N至少3个元素,
所以满足条件的集合M为{1,4,5},{2,4,5},{3,4,5},{1,2,4,5},{1,3,4,5},{2,3,4,5},{1,2,3,4,5},
(3)因为S⊆M,且S中至多含有两个偶数,则比含有2,4,再从1,3,5中任取1有3种,任取2个3个,取3个有1个,共有3+2+1=6个.
点评 考查列举法表示集合,元素与集合的关系,以及子集、真子集的概念.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
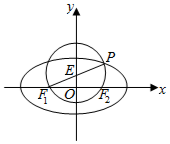 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆E:x2+y2-y-2=0在第一象限相交于点P,椭圆C的左、右焦点F1,F2都在圆E上,且线段PF1为圆E的直径.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆E:x2+y2-y-2=0在第一象限相交于点P,椭圆C的左、右焦点F1,F2都在圆E上,且线段PF1为圆E的直径.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
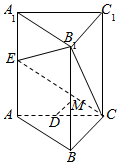 如图,直棱柱ABC-A1B1C1中,AB=AC=2,AA1=BC=2$\sqrt{3}$,E是AA1中点,D是AC的中点,M是BB1上一点,若DM∥平面B1CE,则$\frac{BM}{M{B}_{1}}$=3.
如图,直棱柱ABC-A1B1C1中,AB=AC=2,AA1=BC=2$\sqrt{3}$,E是AA1中点,D是AC的中点,M是BB1上一点,若DM∥平面B1CE,则$\frac{BM}{M{B}_{1}}$=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com