
 如图,在正三棱柱ABC-A1B1C1中(底面为正三角形且侧棱垂直于底面的三棱柱叫正三棱柱),各棱长都是4,D是BC的中点.
如图,在正三棱柱ABC-A1B1C1中(底面为正三角形且侧棱垂直于底面的三棱柱叫正三棱柱),各棱长都是4,D是BC的中点.分析 (I)转化为直线与直线的平行问题证明OD∥A1C,
(II)利用直线与平面的垂直问题确定直线与平面的夹角:∠A1CE为直线A1C与平面BCC1B1所成的角,转化为直角三角形求解.
(III)利用平面直线的性质得出Rt△CDF∽Rt△C1CE,确定∠C1CE+∠CFD=$\frac{π}{2}$,即得证DF⊥CE,DF⊥A1C
判断Rt△ADF在考虑边长关系求解.
解答 解:(Ⅰ)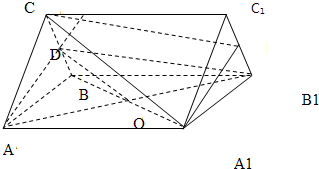
连接A1B交AB1于O,连接OD
∵四边形ABB1A1为正方形
∴O为A1B的中点
又∵D是BC中点
∴OD∥A1C
∵OD?平面AB1D,A1C?平面AB1D
∴A1C∥平面AB1D
(Ⅱ)过A1作A1E⊥B1C1,E,连接CE
∵平面A1B1C1⊥平面BCC1B1
平面A1B1C1∩平面BCC1B1=B1C1
∴A1E⊥平面BCC1B1
∴CE为直线A1C在平面BCC1B1上的投影
∴∠A1CE为直线A1C与平面BCC1B1所成的角,
在Rt△A1C1C中
A1C=$\sqrt{A{C}^{2}+A{{A}_{1}}^{2}}$=$4\sqrt{2}$,
在△A1B1C1中
A1E=2$\sqrt{3}$
在Rt△A1CE中,sin∠A1CE=$\frac{{A}_{1}E}{{A}_{1}C}$=$\frac{\sqrt{6}}{4}$
(Ⅲ)当$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{C{C}_{1}}$时,DF⊥A1C
在正方形BCC1B1中,D,E分别是BC,B1C1的中点
∴$\frac{CD}{C{C}_{1}}$=$\frac{CF}{{C}_{1}E}$=$\frac{1}{2}$,
∴Rt△CDF∽Rt△C1CE
∴∠CDF=∠C1CE
∵∠CDF+∠CFD=$\frac{π}{2}$,
∴∠C1CE+∠CFD=$\frac{π}{2}$,
∴DF⊥CE
由(Ⅱ)可知A1E⊥平面BCC1B1
DF?平面BCC1B1,∴A1E⊥DF
∵A1E∩CE=E,∴DF⊥平面A1CE
∵A1C?平面A1CE
∴DF⊥A1C
在Rt△ADF中 AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=$\sqrt{17}$.
点评 本题考查了直线平面的位置关系,平行,垂直的问题,求解空间角,运算较复杂,对学生的空间思维能力要求较高.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,左右焦点分别为F1、F2,点A(2,$\sqrt{3}$),点F2在线段AF1的中垂线上.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,左右焦点分别为F1、F2,点A(2,$\sqrt{3}$),点F2在线段AF1的中垂线上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=2AB=2,若E,F分别为线段A1D1,CC1的中点,则直线EF与平面ADD1A1所成角的正弦值为( )
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=2AB=2,若E,F分别为线段A1D1,CC1的中点,则直线EF与平面ADD1A1所成角的正弦值为( )| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAC=90°,AB=$\sqrt{3}$,BC=1,AD=AA1=3.
如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAC=90°,AB=$\sqrt{3}$,BC=1,AD=AA1=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BAD=60°.
如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
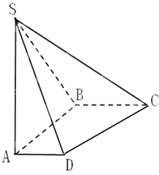 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com