
分析 (Ⅰ)由题意可知,C在线段BA的延长线上,设出A(m,0),B(0,n),可得m2+n2=1,再设C(x,y),由向量等式把m,n用含有x,y的代数式表示,代入m2+n2=1可得点C的轨迹Г;
(Ⅱ)分别设出E,F,K的横坐标分别为:xE,xF,xK,点D(s,t),可得直线PQ的方程为:$\frac{s}{(λ+1)^{2}}x+\frac{t}{{λ}^{2}}y=1$,再设直线m的方程:y=kx+b,得到t=ks+b,进一步求得xK,联立直线方程与椭圆m的方程,利用根与系数的关系得到xE+xF,xExF,求得$\frac{|DK|}{|DE|}+\frac{|DK|}{|DF|}$为定值2得答案.
解答 解:(Ⅰ)由题意可知,C在线段BA的延长线上,
设A(m,0),B(0,n),则m2+n2=1,
再设C(x,y),
由$\overrightarrow{AC}$=λ$\overrightarrow{BA}$(λ>0),得(x-m,y)=λ(m,-n),
∴$\left\{\begin{array}{l}{x-m=λm}\\{y=-λn}\end{array}\right.$,得$\left\{\begin{array}{l}{m=\frac{x}{1+λ}}\\{n=-\frac{y}{λ}}\end{array}\right.$,
代入m2+n2=1,得$\frac{{x}^{2}}{(1+λ)^{2}}+\frac{{y}^{2}}{{λ}^{2}}=1$;
(Ⅱ)设E,F,K的横坐标分别为:xE,xF,xK,
设点D(s,t),则直线PQ的方程为:$\frac{s}{(λ+1)^{2}}x+\frac{t}{{λ}^{2}}y=1$,
设直线m的方程:y=kx+b,
∴t=ks+b,
得${x}_{K}=\frac{1-\frac{t}{{λ}^{2}}b}{\frac{s}{(λ+1)^{2}}+\frac{t}{{λ}^{2}}k}$,
将直线m代入椭圆方程得:$(\frac{{k}^{2}}{{λ}^{2}}+\frac{1}{(λ+1)^{2}}){x}^{2}+\frac{2kb}{{λ}^{2}}x+\frac{{b}^{2}}{{λ}^{2}}-1=0$,
∴${x}_{E}+{x}_{F}=\frac{-2kb}{\frac{{λ}^{2}}{(λ+1)^{2}}+{k}^{2}},{x}_{E}{x}_{F}$=$\frac{{b}^{2}-{λ}^{2}}{\frac{{λ}^{2}}{(λ+1)^{2}}+{k}^{2}}$.
∴$\frac{|DK|}{|DE|}+\frac{|DK|}{|DF|}=\frac{|{x}_{D}-{x}_{K}|}{|{x}_{D}-{x}_{E}|}+\frac{|{x}_{D}-{x}_{K}|}{|{x}_{D}-{x}_{F}|}$=$|s-\frac{1-\frac{t}{{λ}^{2}}b}{\frac{s}{(λ+1)^{2}}+\frac{t}{{λ}^{2}}k}|$•$\frac{|2{x}_{D}-({x}_{E}+{x}_{F})|}{{|{x}_{D}}^{2}-{x}_{D}({x}_{E}+{x}_{F})+{x}_{E}{x}_{F}|}$=2.
验经证当m的斜率不存在时成立,
故存在实数t=2,使得$\frac{1}{|DE|}$+$\frac{1}{|DF|}$=$\frac{t}{|DK|}$恒成立.
点评 本题考查轨迹方程的求法,考查了直线与圆锥曲线的位置关系,考查计算能力,是压轴题.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 向右平移1个单位,再向下平移2个单位 | |
| B. | 向右平移1个单位,再向上平移2个单位 | |
| C. | 向左平移1个单位,再向上平移2个单位 | |
| D. | 向左平移1个单位,再向下平移2个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2或$-\frac{5}{2}$ | C. | 2或-2 | D. | 2或-2或$-\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
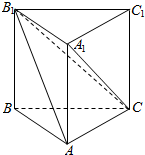 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com