Question

13．设抛物线C：y²=2px（p＞0）的焦点为F，其准线与x轴的交点为Q，过Q点的直线1交抛物线于A，B两点．
（1）若以AB为直径的圆恰好过点F，求直线1的斜率；
（2）设直线AF，BF与抛物线C的另一个交点分别为D，E，求证：|AB|=|DE|．

Answer 1

分析 （1）求出抛物线的焦点和准线方程，由点斜式写出直线l的方程，和抛物线方程联立后化为关于x的一元二次方程，利用根与系数关系求出A，B两点的横坐标的和与积，写出向量$\overrightarrow{FA}$，$\overrightarrow{FB}$的坐标，由向量垂直的条件，展开数量积后代入根与系数关系得答案；
（2）设直线l的方程为l：x=ky-$\frac{p}{2}$，和抛物线方程联立后化为关于y的一元二次方程，写出根与系数关系，由两点式求出斜率后作和化简，代入根与系数关系，由对称性即可得到答案．

解答 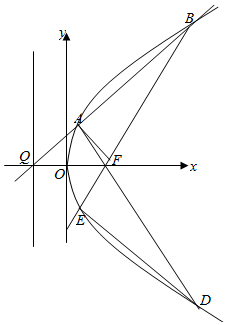解：（1）抛物线C：y²=2px（p＞0）的焦点为F（$\frac{p}{2}$，0），
准线方程为x=-$\frac{p}{2}$，即有Q（-$\frac{p}{2}$，0）
由题意可得l：y=k（x+$\frac{p}{2}$），
联立$\left\{\begin{array}{l}{y=k（x+\frac{p}{2}）}\\{{y}^{2}=2px}\end{array}\right.$，得k²x²+（k²-2）px+$\frac{{k}^{2}{p}^{2}}{4}$=0．
设A（x₁，y₁），B（x₂，y₂），
x₁+x₂=-$\frac{（{k}^{2}-2）p}{{k}^{2}}$，x₁x₂=$\frac{{p}^{2}}{4}$．
则$\overrightarrow{FA}$=（x₁-$\frac{p}{2}$，y₁），$\overrightarrow{FB}$=（x₂-$\frac{P}{2}$，y₂）．
以AB为直径的圆恰好过点F，
可得$\overrightarrow{FA}$•$\overrightarrow{FB}$=（x₁-$\frac{P}{2}$）（x₂-$\frac{P}{2}$）+y₁y₂
=（1+k²）x₁x₂-$\frac{p}{2}$（1-k²）（x₁+x₂）+$\frac{{p}^{2}}{4}$（1+k²）=0，
即有 （1+k²）•$\frac{{p}^{2}}{4}$-$\frac{p}{2}$（1-k²）（-$\frac{（{k}^{2}-2）p}{{k}^{2}}$）+$\frac{{p}^{2}}{4}$（1+k²）=0，
化为k²（1+k²）+（1-k²）（k²-2）=0，
解得k=±$\frac{\sqrt{2}}{2}$；
（2）证明：设直线l：x=ky-$\frac{p}{2}$，
与抛物线联立得y²-2pky+p²=0．
设A（x₁，y₁），B（x₂，y₂），
∴y₁+y₂=2pk，y₁y₂=p²．
则k₁+k₂=$\frac{{y}_{1}}{{x}_{1}-\frac{p}{2}}$+$\frac{{y}_{2}}{{x}_{2}-\frac{p}{2}}$
=$\frac{{y}_{1}}{k{y}_{1}-p}$+$\frac{{y}_{2}}{k{y}_{2}-p}$=$\frac{2k{y}_{1}{y}_{2}-p（{y}_{1}+{y}_{2}）}{（k{y}_{1}-p）（k{y}_{2}-p）}$
=$\frac{2k{p}^{2}-p•2pk}{（k{y}_{1}-p）（k{y}_{2}-p）}$=0，
可得直线AF，BF关于x轴对称，
再由抛物线关于x轴对称，
可得|AB|=|DE|．

点评 本题考查了抛物线的简单几何性质，考查了直线与圆锥曲线的关系，涉及直线与圆锥曲线的关系问题，常利用一元二次方程的根与系数关系，采用设而不求的方法解决，此题属中档题．